Question

【题目】如图,已知线段a,直线AB和CD相交于点O.利用尺规按下列要求作图：

（1）在射线OA、OB、OC、OD上作线段OA′、OB′、OC′、OD′，使它们分别与线段a相等；

（2）连接A′C′、C′B′、B′D′、D′A′.你得到了一个怎样的图形？

Answer 1

【答案】（1）如图，见解析；（2）得到的四边形是正方形

【解析】

（1）以点O为圆心，a为半径作圆，分别交射线OA，OB，OC，OD于A′、B′、C′、D′；（2）利用对角线互相垂直平分且相等可判断四边形A′C′B′D′为正方形．

解：（1）如图，以点O为圆心，a为半径作圆，分别交射线OA，OB，OC，OD于A′、B′、C′、D′；

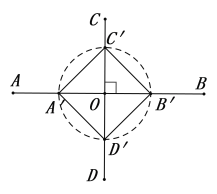
（2）得到的四边形四边形A′C′B′D′是正方形，理由如下：

∵OA′=OB′=a，OC′=OD′=a，

∴四边形A′C′B′D′是平行四边形，

∵OA′=OB′=OC′=OD′=a，

∴A′B′=C′D′，

∴四边形A′C′B′D′是矩形，

∵A′B′⊥C′D′，

∴四边形A′C′B′D′是正方形.