题目内容
【题目】如图，在6×8的网格纸中，每个小正方形的边长都为1，动点P、Q分别从点D、A同时出发向右移动，点P的运动速度为每秒2个单位，点Q的运动速度为每秒1个单位，当点P运动到点C时，两个点都停止运动.运动时间t 为_______秒时，△PQB成为以PQ为腰的等腰三角形.
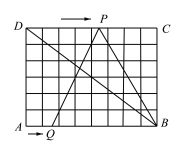
【答案】
或
【解析】
作QS⊥FE于S， △PQB是以PQ为腰的等腰三角形分以下两种情况分别求解，①当PB=PQ时，由
；②当QB=QP时，
QB=8-t，求解即可
解：如图：作QS⊥FE于S
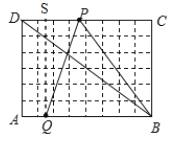
由题意得：PD=2t，AQ=t，则PS=2t-t=t
在Rt△PSQ中，
，
∴
①当PB=PQ时，；
解得：t=或8（舍去）
②当QB=QP时，
解得：t=
故运动时间为或秒时，△PQB是以PQ为腰的等腰三角形.
练习册系列答案
相关题目
【题目】乐乐根据学习函数的经验，对函数y=|x-1|的图象与性质进行了研究，下面是乐乐的研究过程，请补充完成:
(1)函数y=|x-1|的自变量x的取值范围是 .
(2)列表，找出y与x的几组对应值.
x | … | -1 | 0 | 1 | 2 | 3 | … |
y | … | b | 1 | 0 | 1 | 2 | … |
(3)在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，并画出该函数的图象.
(4)①函数的最小值为 ；
②写出一条该函数的其它性质: .
