题目内容
【题目】在8×8的正方形网格中建立如图所示的平面直角坐标系，已知A（2，4），B（4，2）．C是第一象限内的一个格点，由点C与线段AB组成一个以AB为底，且腰长为无理数的等腰三角形．C点的坐标是 ， △ABC的面积为 ．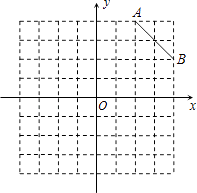 
【答案】（1，1）；4
【解析】解：根据题意点C坐标为（1，1），S△ABC=3×3﹣ 
×3×1﹣ ×3×1﹣ ×2×2=4． 所以答案是（1，1），4
【考点精析】关于本题考查的无理数和勾股定理的概念，需要了解在理解无理数时，要抓住“无限不循环”这个要点，归纳起来有四类：（1）开方开不尽的数；（2）有特定意义的数，如圆周率π，或化简后含有π的数；（3）有特定结构的数，如0.1010010001…等；（4）某些三角函数，如sin60o等；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
【题目】盛盛同学到某高校游玩时，看到运动场的宣传栏中的部分信息（如下表）：
院系篮球赛成绩公告 | |||
比赛场次 | 胜场 | 负场 | 积分 |
22 | 12 | 10 | 34 |
22 | 14 | 8 | 36 |
22 | 0 | 22 | 22 |
盛盛同学结合学习的知识设计了如下问题，请你帮忙完成下列问题：
（1）从表中可以看出，负一场积______分,胜一场积_______分；
（2）某队在比完22场的前提下，胜场总积分能等于其负场总积分的2倍吗？请说明理由.
