题目内容
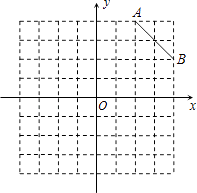
【题目】如图，图中的小方格都是边长为1的正方形，△ABC与△A′B′C′的顶点都在格点上．
（1）求证：△ABC∽A′B′C′；
（2）A′B′C′与△ABC是位似图形吗？如果是，在图形上画出位似中心并求出位似比．
【答案】
（1）
证明：∵AB= 
，BC= 
，AC=2 ，A′B′=2 ，B′C′=2 ，A′C′=4 ，
∴ 
= 
= 
= 
，
∴△ABC∽A′B′C′
（2）
解：如图所示：两三角形对应点的连线相交于一点，故A′B′C′与△ABC是位似图形，O即为位似中心，
位似比为：2．
【解析】（1）分别求出三角形各边长，进而得出答案；（2）利用位似图形的性质得出答案．
【考点精析】根据题目的已知条件，利用作图-位似变换的相关知识可以得到问题的答案，需要掌握对应点到位似中心的距离比就是位似比，对应线段的比等于位似比，位似比也有顺序；已知图形的位似图形有两个，在位似中心的两侧各有一个．位似中心，位似比是它的两要素．
练习册系列答案
名校联盟快乐课堂系列答案
黄冈创优卷系列答案
相关题目
