题目内容
【题目】如图，在平面直角坐标系中，等腰三角形ABO的底边OA在x轴上，顶点B在反比例函数y= 
（x＞0）的图象上，当底边OA上的点A在x轴的正半轴上自左向右移动时，顶点B也随之在反比例函数y= （x＞0）的图象上滑动，但点O始终位于原点．
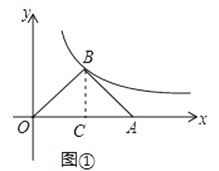
（1）如图①，若点A的坐标为（6，0），求点B的坐标；
（2）当点A移动到什么位置时，三角形ABO变成等腰直角三角形，请说明理由；
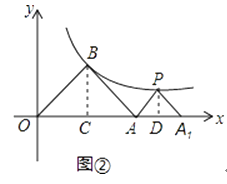
（3）在（2）中，如图②，△PA1A是等腰直角三角形，点P在反比例函数y= （x＞0）的图象上，斜边A1A在x轴上，求点A1的坐标．
【答案】
（1）
解：如图①，过点B作BC⊥x轴于点C，
∵OB=AB，
∴OC=AC，点A移动到什么位置时，三角形ABO变成等腰直角三角形，
∵点A的坐标为（6，0），
∴OC= 
OA=3，
∵顶点B在反比例函数y= 
（x＞0）的图象上，
∴y= 
=4，
∴点B的坐标为：（3，4）
（2）
解：点A移动到（4 
，0）时，△ABO变成等腰直角三角形．
理由：如图②，过点B作BC⊥x轴于点C，
∵△AOB是等腰直角三角形，
∴BC=OC= OA，
设点B（a，a），
∵顶点B在反比例函数y= （x＞0）的图象上，
∴a= 
，
解得：a=±2 （负值舍去），
∴OC=2 ，
∴OA=2OC=4 ，
∴点A移动到（4 ，0）时，△ABO变成等腰直角三角形
（3）
解：如图②，过点P作PD⊥x轴于点D，
∵△PA1A是等腰直角三角形，
∴PD=AD，
设AD=b，则点P（4 +b，b），
∵点P在反比例函数y= （x＞0）的图象上，
∴b= 
，
解得：b1=2 
﹣2 ，b2=﹣2 ﹣2 （舍去），
∴AA1=2b=4 ﹣4 ，
∴OA1=OA+AA1=4 ，
∴点A1的坐标为：（4 ，0）．
【解析】（1）首先过点B作BC⊥x轴于点C，由等腰三角形的三线合一，可得OC=AC=3，然后由顶点B在反比例函数y= （x＞0）的图象上，求得点B的坐标；（2）首先由等腰直角三角形的性质，可得OC=BC，然后由顶点B在反比例函数y= （x＞0）的图象上，求得点B的坐标，继而求得点A的坐标；（3）首先过点P作PD⊥x轴于点D，易得AD=PD，则可设AD=b，则点P（4 +b，b），又由点P在反比例函数y= （x＞0）的图象上，求得b的值，继而求得答案．
