题目内容
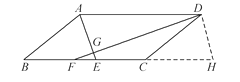
【题目】已知:如图,在ABCD中,∠ADC,∠DAB的平分线DF,AE分别与线段BC相交于点F,E,DF与AE相交于点G.
(1)求证:AE⊥DF;
(2)若AD=10,AB=6,AE=4,求DF的长.

【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)根据平行四边形的性质和平行线的性质推出∠ADC+∠DAB=180°,根据角平分线得到∠ADF+∠DAE=![]() (∠ADC+∠DAB)=90°,即可求出结论;
(∠ADC+∠DAB)=90°,即可求出结论;
(2)过点D作DH∥AE,交BC的延长线于点H,得到平行四边形AEHD,求出DH=AE=4,EH=AD=10,根据平行四边形的性质和平行线的性质推出DC=FC,AB=EB,求出BF、FE、FH的长,根据勾股定理即可求出答案.
试题解析:(1)∵在ABCD中,AB∥CD,
∴∠ADC+∠DAB=180°,
∵DF,AE分别是∠ADC,∠DAB的平分线,
∴∠ADF=∠CDF=![]() ∠ADC,∠DAE=∠BAE=
∠ADC,∠DAE=∠BAE=![]() ∠DAB,
∠DAB,
∴∠ADF+∠DAE=![]() (∠ADC+∠DAB)=90°,
(∠ADC+∠DAB)=90°,
∴∠AGD=90°,即AE⊥DF;
(2)如图,过点D作DH∥AE,交BC的延长线于点H,则四边形AEHD是平行四边形,且FD⊥DH,
∴DH=AE=4,EH=AD=10,
∵在ABCD中,AD∥BC,∴∠ADF=∠CFD,∠DAE=∠BEA,
∴∠CDF=∠CFD,∠BAE=∠BEA,
∴DC=FC,AB=EB,
在ABCD中,AD=BC=10,AB=DC=6,∴CF=BE=6,BF=BC-CF=10-6=4,
∴FE=BE-BF=6-4=2,∴FH=FE+EH=12,
在Rt△FDH中,DF=![]() .
.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目