Question

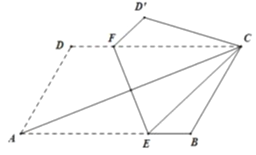
【题目】如图，将平行四边形沿对折，使点落在点处，若，则到的距离为____________.

Answer 1

【答案】

【解析】分析：过点C作CM⊥AB的延长线于点M，根据翻折的性质，设AE=x，CE=x，BE=6-x，EM=8-x，在△CEM中，利用勾股定理列出方程即可求出x的值．然后算出三角形CBE的面积，根据等面积法即可求出点B到CE的距离.

详解：作CM⊥AB于M，如图所示：

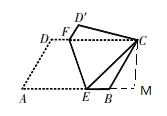
则∠M=90°，

∵四边形ABCD是平行四边形，

∴BC=AD=4，BC∥AD，

∴∠CBM=∠A=60°，

∴∠BCM=30°，

∴BM=BC=4×=2.

在Rt△BMC中，根据勾股定理可得CM=2.

设AE=x，则CE=x，BE=6-x，EM=8-x，

∵CE2=CM2+EM2，

∴x2=(2)2+(8-x)2，

解得：x=，

∴CE=,BE=6-=,

∴S△CBE=.

∴点B到CE的距离= S△CBE÷CE×2=.