题目内容
【题目】（背景）某班在一次数学实践活动中，对矩形纸片进行折叠实践操作，并将其产生的数学问题进行相关探究． （操作）如图，在矩形ABCD中，AD=6，AB=4，点P是BC边上一点，现将△APB沿AP对折，得△APM，显然点M位置随P点位置变化而发生改变
（问题）试求下列几种情况下：点M到直线CD的距离
（1）∠APB=75°；
（2）P与C重合；
（3）P是BC的中点．
【答案】
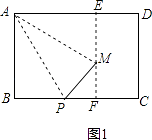
（1）解：当∠APB=75°时，如图1，过M作EF⊥AD，则EF⊥BC，
∵∠AMP=∠B=∠MFP=90°，
∴∠AME=∠MPF，
∴△AEM∽△MFP，
∵∠APB=75°，
∴∠MPF=30°，
∵AM=AB=4，
∴AE=2，
∴DE=4
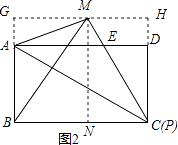
（2）解：当P与C重合，如图2，过M作GH∥AD交BA，CD的延长线于G，H，
则四边形ADHG是矩形，
∵∠AMP=∠ABC=∠AMC=90°，
∴∠AMG=∠MPH，
∴△AMG∽△MHP，
设AG=x，则DH=x，
∴PH=4+x，
∴ 
，
∴MH= 
x，
在Rt△MHP中，MH2+PH2=MC2，
即（ x）2+（4x）2=62，
∴x= 
（负值舍去），
∴MH= 
（3）解：当P是BC的中点时，如图3，过M作EF∥AB交AB，BC于E，F，
∵P是BC的中点，
∴BP=3，
设PF=x，则BF=3+x，
∴AE=3+x，
由折叠的性质得，AM=AB=4，PM=PB=3，∠AMP=∠B=90°，
∴△AEM∽△MFP，
∴ 
，
∴EM= 
x，
在Rt△AEM中，
AE2+EM2=AM2，
即（ x）2+（3+x）2=42，
∴x= 
（负值舍去），
∴DE= 
．
【解析】（1）如图1，过M作EF⊥AD，则EF⊥BC，由∠AMP=∠B=∠MFP=90°，得到∠AME=∠MPF，推出△AEM∽△MFP，根据已知条件得到∠MPF=30°，AE=2，即可得到结论；（2）如图2，过M作GH∥AD交BA，CD的延长线于G，H，则四边形ADHG是矩形，推出△AMG∽△MHP，设AG=x，则DH=x，得到PH=4+x，列比例式得到MH= x，根据勾股定理得到x= （负值舍去），即可得到结论；（3）当P是BC的中点时，如图3，过M作EF∥AB交AB，BC于E，F，推出△AEM∽△MFP，根据相似三角形的性质得到 ，得到EM= x，根据勾股定理列方程即可得到结论．
【考点精析】根据题目的已知条件，利用翻折变换（折叠问题）的相关知识可以得到问题的答案，需要掌握折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．
