Question

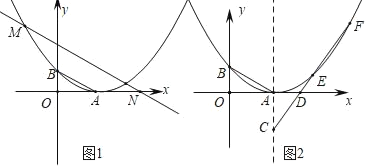
【题目】如图1，已知在矩形中，，是上一点，且，点是上一点，，．

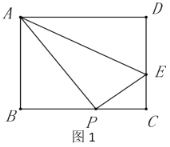
（1）求证：；

（2）求的长；

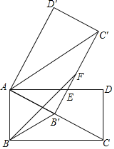
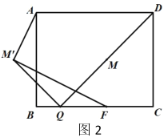
（3）如图2，点在边上且，点是边上的一动点，且从点向点方向运动．连接，是的中点，将点绕点逆时针旋转90°，点的对应点是，在点的运动过程中，①判断是否为定值？若是说明理由．②求的最小值．

Answer 1

【答案】（1）证明见解析；（2）；（3）①不变，见解析，②

【解析】

（1）由SAS证明△APE≌△ADE得出∠APE＝∠D＝90°即可；

（2）由全等三角形的性质得出PE＝DE＝5，设BP＝x，则PC＝10x，证明△ABP∽△PCE，得出，得出AB＝202x，CE＝x，由AB＝CD得出方程，解方程即可得出结果；

（3）①作MG⊥B于G，M'H⊥BC于H，证明△HQM'≌△GMQ得出HM'＝GQ，QH＝MG＝4，设HM'＝x，则CG＝GQ＝x，FG＝4x，求出QF＝GQFG＝2x4，得出FH＝QH＋QF＝2x，由三角函数得出tan∠∠M′FB＝，即可得出结论；

②当AM'⊥FM'时，AM'的值最小，延长HM'交DA延长线于N，则NH＝AB＝8，NM'＝8x，AN＝BH＝HQBQ＝2x6，同①得：△ANM'∽△M'HF，得出，解得：x＝4，得出AN＝2，NM'＝4，在Rt△ANM'中，由勾股定理即可得出结果．

（1）证明：∵四边形ABCD是矩形，

∴BC＝AD＝10，AB＝CD，∠B＝∠C＝∠D＝90°，

∵AD＝10，PA＝10，∠PAD＝2∠DAE，

∴AP＝AD，∠PAE＝∠DAE，

在△APE和△ADE中，

，

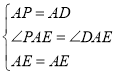∴△APE≌△ADE（SAS），

∴∠APE＝∠D＝90°；

（2）解：由（1）得：△APE≌△ADE，

∴PE＝DE＝5，

设BP＝x，则PC＝10x，

∵∠B＝90°，∠APE＝90°，

∴∠BAP＋∠APB＝90°，∠APB＋∠CPE＝90°，

∴∠BAP＝∠CPE，

∴△ABP∽△PCE，

∴，即＝2，

∴AB＝202x，CE＝x，

∵AB＝CD，

∴202x＝5＋x，

解得：x＝6，

∴AB＝202x＝8；

（3）解：①∠M′FB为定值，理由如下：

作MG⊥B于G，M'H⊥BC于H，如图2所示：

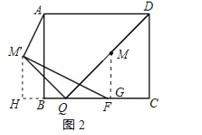
则MG∥CD，∠H＝∠MGQ＝90°，

∴∠QMG＋∠MQG＝90°，

∵M是DQ的中点，

∴QG＝CG，

∴MG是△CDQ的中位线，

∴MG＝CD＝AB＝4，

由旋转的性质，QM'＝QM，∠M'QM＝90°，

∴∠HQM'＋∠MQG＝90°，

∴∠HQM'＝∠QMG，

在△HQM'和△GMQ中，

，

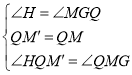∴△HQM'≌△GMQ（ASA），

∴HM'＝GQ，QH＝MG＝4，

设HM'＝x，则CG＝GQ＝x，

∴FG＝4x，

∴QF＝GQFG＝2x（4x）＝2x4，

∴FH＝QH＋QF＝2x，

∴tan∠M′FB＝，

∴∠M′FB为定值；

②当AM'⊥FM'时，AM'的值最小，延长HM'交DA延长线于N，如图3所示：

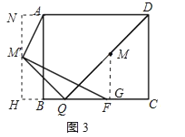
则NH＝AB＝8，NM'＝8x，AN＝BH＝HQBQ＝4（102x）＝2x6，

同①得：△ANM'∽△M'HF，

∴，

∴，

解得：x＝4，

∴AN＝2，NM'＝4，

在Rt△ANM'中，由勾股定理得：AM'＝．