题目内容
【题目】在
中，
是边
上的两点，
，
，则
的度数是____________．
【答案】110°或70°
【解析】
先分△ABC为锐角三角形和钝角三角形两种情况画出图形，然后根据三角形内角和定理可求∠AED+∠ADE，再根据三角形外角的性质和等腰三角形的性质可求∠BAE+∠CAD，再根据角的和差关系即可求解．
解：①如图1，当△ABC为钝角三角形时，
∵∠EAD=40°，∴∠AED+∠ADE=140°，
∵EA=EB，DA=DC，
∴∠B=∠BAE，∠C=∠CAD，
∵∠AED+∠ADE=∠B+∠BAE+∠C+∠CAD=140°，
∴∠BAE+∠CAD=70°，
∴∠BAC=110°．
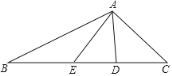
图1
②如图2，当△ABC为锐角三角形时，
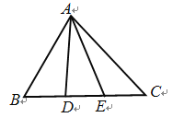
图2
同①方法可求得∠BAE+∠CAD=110°，
∴∠BAC=∠BAE+∠CAD-∠DAE=110°-40°=70°.
故答案为：110°或70°．
练习册系列答案
相关题目
