题目内容
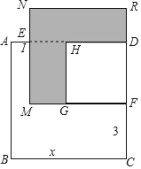
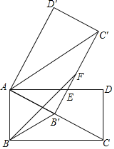
【题目】如图,矩形![]() 中,
中,![]() ,将矩形
,将矩形![]() 绕点
绕点![]() 旋转得到矩形
旋转得到矩形![]() ,使点
,使点![]() 的对应点
的对应点![]() 落在
落在![]() 上,
上,![]() 交
交![]() 于点
于点![]() ,在
,在![]() 上取点
上取点![]() ,使
,使![]() .
.
(1)证:![]() .
.
(2)![]() 的度数.
的度数.
(3)知![]() ,求
,求![]() 的长.
的长.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)在直角三角形ABC中,由AC=2AB,得到∠ACB=30°,再由折叠的性质得到一对角相等,利用等角对等边即可得证;
(2)由(1)得到△ABB′为等边三角形,利用矩形的性质及等边三角形的内角为60°,即可求出所求角度数;
(3)连接AF,过A作AM⊥BF,可得△AB′F是等腰直角三角形,△AB′B为等边三角形,分别利用三角函数定义求出MF与AM,根据AM=BM,即BM+MF=BF即可求出.
(1)证明:∵在![]() 中,
中,![]() ,
,
∴![]() ,
,![]() ,
,
由旋转可得:![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)解:由(1)得到△ABB′为等边三角形,
∴∠AB′B=60°,即∠BB'F=∠AB'B+∠AB'F=150°,
∵BB'=B'F,
∴∠FBB′=∠B'FB=15°;
(3)连接![]() ,过
,过![]() 作
作![]() ,由(2)可得
,由(2)可得![]() 是等腰直角三角形,
是等腰直角三角形,![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
则![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目