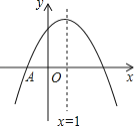题目内容
【题目】在平面直角坐标系中,抛物线y![]() x2沿x轴正方向平移后经过点A(x1,y2),B(x2,y2),其中x1,x2是方程x2﹣2x=0的两根,且x1>x2,
x2沿x轴正方向平移后经过点A(x1,y2),B(x2,y2),其中x1,x2是方程x2﹣2x=0的两根,且x1>x2,
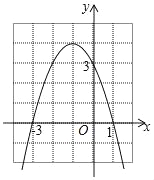
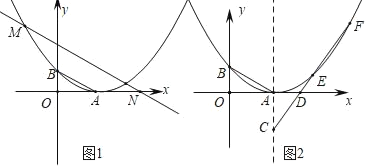
(1)如图.求A,B两点的坐标及平移后抛物线的解析式;
(2)平移直线AB交抛物线于M,交x轴于N,且![]() ,求△MNO的面积;
,求△MNO的面积;
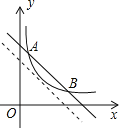
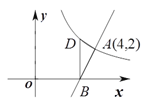
(3)如图,点C为抛物线对称轴上顶点下方的一点,过点C作直线交抛物线于E、F,交x轴于点D,探究![]() 的值是否为定值?如果是,求出其值;如果不是,请说明理由.
的值是否为定值?如果是,求出其值;如果不是,请说明理由.
【答案】(1)点A坐标为(2,0),点B坐标为(0,1),![]() ;(2)12或28;(3)
;(2)12或28;(3)![]() 为定值,定值为1.
为定值,定值为1.
【解析】
(1)解方程x2﹣2x=0得x1=2,x2=0.即可求得点A坐标为(2,0),抛物线解析式为![]() ,把x=0代入抛物线解析式得y=1,即可得点B坐标为(0,1);(2)如图,过M作MH⊥x轴,垂足为H,由AB∥MN,即可得△ABO∽△MHN,根据相似三角形的性质可得
,把x=0代入抛物线解析式得y=1,即可得点B坐标为(0,1);(2)如图,过M作MH⊥x轴,垂足为H,由AB∥MN,即可得△ABO∽△MHN,根据相似三角形的性质可得![]() ,由此求得MH=4,HN=8,将y=4代入抛物线
,由此求得MH=4,HN=8,将y=4代入抛物线![]() 求得x1=﹣2,x2=6,所以M1(﹣2,4),N1(6,0),M2(6,4),N2(14,0),由此求得△MNO的面积即可;(3)设C(2,m),求得CD解析式为y=kx+m﹣2k,令y=0得kx+m﹣2k=0,由此求得点D为(
求得x1=﹣2,x2=6,所以M1(﹣2,4),N1(6,0),M2(6,4),N2(14,0),由此求得△MNO的面积即可;(3)设C(2,m),求得CD解析式为y=kx+m﹣2k,令y=0得kx+m﹣2k=0,由此求得点D为(![]() ,0);把CD的解析式与抛物线的解析式联立
,0);把CD的解析式与抛物线的解析式联立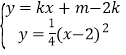 ,消去y得,kx+m﹣2k=
,消去y得,kx+m﹣2k=![]() (x﹣2)2.化简得x2﹣4(k+1)x+4﹣4m+8k=0,由根与系数关系得,x1+x2=4k+4,x1x2=4﹣4m+8k.过E、F分别作EP⊥CA于P,FQ⊥CA于Q,由AD∥EP,AD∥FQ,可得
(x﹣2)2.化简得x2﹣4(k+1)x+4﹣4m+8k=0,由根与系数关系得,x1+x2=4k+4,x1x2=4﹣4m+8k.过E、F分别作EP⊥CA于P,FQ⊥CA于Q,由AD∥EP,AD∥FQ,可得![]() =
=![]() =(
=(![]() ﹣2)×
﹣2)×![]() =
=![]() =1,由此可得
=1,由此可得![]() 为定值,定值为1.
为定值,定值为1.
(1)解方程x2﹣2x=0得x1=2,x2=0.
∴点A坐标为(2,0),抛物线解析式为![]() .
.
把x=0代入抛物线解析式得y=1.
∴点B坐标为(0,1).
(2)如图,过M作MH⊥x轴,垂足为H
∵AB∥MN
∴△ABO∽△MHN
∴![]()
∴MH=4,HN=8
将y=4代入抛物线![]()
可得x1=﹣2,x2=6
∴M1(﹣2,4),N1(6,0),M2(6,4),N2(14,0),
∴![]()
![]()
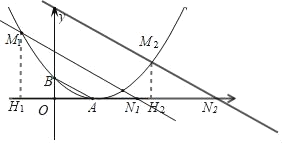
(3)设C(2,m),设直线CD为y=kx+b
将C(2,m)代入上式,m=2k+b,即b=m﹣2k.
∴CD解析式为y=kx+m﹣2k,
令y=0得kx+m﹣2k=0,
∴点D为(![]() ,0)
,0)
联立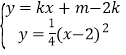 ,
,
消去y得,kx+m﹣2k=![]() (x﹣2)2.
(x﹣2)2.
化简得,x2﹣4(k+1)x+4﹣4m+8k=0
由根与系数关系得,x1+x2=4k+4,x1x2=4﹣4m+8k.
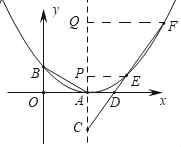
过E、F分别作EP⊥CA于P,FQ⊥CA于Q,
∴AD∥EP,AD∥FQ,
∴![]() =
=![]()
=(![]() ﹣2)×
﹣2)×![]()
=![]()
=1
∴![]() 为定值,定值为1.
为定值,定值为1.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案