题目内容
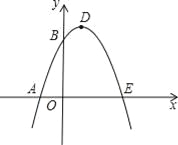
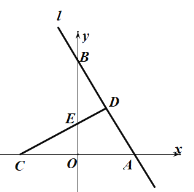
【题目】如图，在平面直角坐标系中，l是经过A（2，0），B（0，b）两点的直线，且b0，点C的坐标为（2，0），当点B移动时，过点C作CD⊥l交于点D．
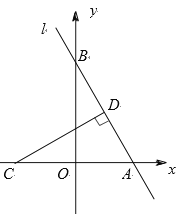
（1）求点D，O之间的距离；
（2）当tan∠CDO=
时，求直线l的解析式；
（3）在（2）的条件下，直接写出△ACD与△AOB重叠部分的面积．
【答案】（1）2；（2）
；（3）
【解析】
（1）直接利用直角三角形斜边中线的性质即可得出答案；
（2）通过等量代换得出
，进而求出点B的坐标，然后利用待定系数法求解即可；
（3）先通过正切和勾股定理求出OE,AD,CD的长度，然后利用
即可求解．
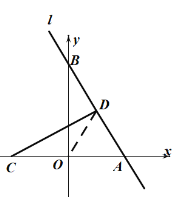
解：（1）连接OD，
，
．
，
，
；
（2）
，
．
，
．
，
，
．
，
，
，
．
设直线l的解析式为
，
将
代入解析式中得
，
解得
，
∴直线l解析式为；
（3）设CD与y轴的交点为E，
，
，
，
．
，
，
∴△ACD与△AOB重叠部分的面积为
．
练习册系列答案
英才点津系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
