题目内容
【题目】如图,AE∥BF,AC平分∠BAD,交BF于点C,BD平分∠ABC,交AE于点D,连接CD. 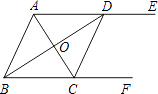
(1)若AB=1,则BC的长=;
(2)求证:四边形ABCD是菱形.
【答案】
(1)1
(2)证明:∵AC平分∠BAD,
∴∠BAC=∠CAD,
∵AD∥BC,
∴∠DAC=∠BCA,
∴∠BAC=∠BCA,
∴BC=BA,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵AD∥BC,
∴∠ADB=∠BDC,
∴∠ABD=∠ADB,
∴AB=AD,
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∵AB=AD,
∴四边形ABCD是菱形.
【解析】(1)解:∵AC平分∠BAD, ∴∠BAC=∠CAD,
∵AD∥BC,
∴∠DAC=∠BCA,
∴∠BAC=∠BCA,
∴BC=BA=1.
所以答案是1.
【考点精析】解答此题的关键在于理解菱形的判定方法的相关知识,掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目