题目内容
【题目】顶角为36°的等腰三角形称为黄金三角形,利用黄金三角形求![]() 的准确值.
的准确值.
【答案】![]()
【解析】
根据黄金三角形的顶角为36°,利用等腰三角形的性质求证∠GBC=∠BAC,∠C=∠C,从而得到△BGC∽△ABC,然后利用相似三角形的性质求其底与一腰之比即![]() ,作出黄金三角形顶角的平分线,解得等腰三角形三线合一的性质即可得出sin18°的值
,作出黄金三角形顶角的平分线,解得等腰三角形三线合一的性质即可得出sin18°的值
解:如图所示:做MN垂直平分AB交AC于点G,作∠BAC的平分线AD,
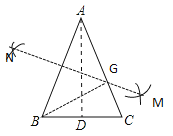
∵△ABC是黄金三角形,
∴∠BAC=36°,AB=AC,
∴AG=BG,∠GBA=∠BAG=36°,∠ABC=∠C=72°
∴∠GBC=36°,∠BGC=72°
设BC=x,AB=AC=y,
∴AG=BG=BC=x.
∵∠GBC=∠BAC,∠C=∠C,
∴△BGC∽△ABC,
∴![]() ,即
,即![]() ,
,
整理,得x2+xy-y2=0,
解得![]()
因为x、y均为正数,所以![]()
即![]() ,
,
作∠BAC的平分线AD,
则∠BAD=∠CAD=![]() ∠BAC=18°,AD⊥BC,BD=CD=
∠BAC=18°,AD⊥BC,BD=CD=![]() BC,
BC,
在Rt△ABD中,∠ADB=90°,
∴sin18°=sin∠BAD=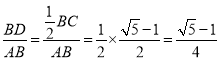 .
.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目