题目内容
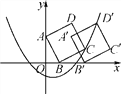
【题目】如图,在平面直角坐标系中,正方形ABCD的顶点A、B的坐标分别为(0,2)、(1,0),顶点C在函数y=![]() x2+bx-1的图象上,将正方形ABCD沿x轴正方向平移后得到正方形A′B′C′D′,点D的对应点D′落在抛物线上,则点D与其对应点D′之间的距离为 ______.
x2+bx-1的图象上,将正方形ABCD沿x轴正方向平移后得到正方形A′B′C′D′,点D的对应点D′落在抛物线上,则点D与其对应点D′之间的距离为 ______.
【答案】2
【解析】如图,过C作GH⊥x轴,交x轴于G,过D作DH⊥GH于H,由正方形的性质和A、B点的坐标证得△AOB≌△BGC,然后根据全等三角形的性质求得C点(3,1),利用点C的坐标代入函数的解析式y=![]() x2+bx-1,求得b=-
x2+bx-1,求得b=-![]() ,同理得到△AOB≌△BGC,得出D的坐标(2,3),根据平移的性质:D、D′纵坐标相同,则y=3,代入函数的解析式
,同理得到△AOB≌△BGC,得出D的坐标(2,3),根据平移的性质:D、D′纵坐标相同,则y=3,代入函数的解析式![]() x2-
x2-![]() x-1=3,解得x=4或x=-3(舍去),求出D′点的坐标为(4,3),即可得D与D′的距离为2.
x-1=3,解得x=4或x=-3(舍去),求出D′点的坐标为(4,3),即可得D与D′的距离为2.
故答案为:2.


练习册系列答案
相关题目