题目内容
【题目】如图，正方形ABCD中，E是AD的中点，AB=8 
，F是线段CE上的动点，则BF的最小值是（ ）
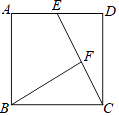
A.10
B.12
C.16
D.18
【答案】C
【解析】解：当BF⊥EC时，BF有最小值，如图，
则∠BFC=90°，
∵E是AD的中点，
∴ED= 
AD= × 
=4 
，
∵四边形ABCD是正方形，
∴∠D=90°，BC=CD=AB=8 ，
Rt△EDC中，由勾股定理得：EC= 
=20，
∵∠BFC=∠D=90°，∠FBC=∠ECD，
∴△BFC∽△CDE，
∴ 
，
∴ 
= 
，
∴BF=16，
所以答案是：C．
【考点精析】通过灵活运用正方形的性质和相似三角形的判定与性质，掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方即可以解答此题．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
【题目】某集团购买了150吨物资打算运往某地支援，现有甲、乙、丙三种车型供选择，每辆汽车的运载能力和运费如下表所示：（假设每辆车均满载）
车型 | 甲 | 乙 | 丙 |
汽车运载量（吨/辆） | 5 | 8 | 10 |
汽车运费（元/辆） | 1000 | 1200 | 1500 |
（1）若全部物资都用甲、乙两种车型来运送，需运费24000元，问分别需甲、乙两种车型各多少辆？
（2）若该集团决定用甲、乙、丙三种汽车共18辆同时参与运送，请你写出可能的运送方案，并帮助该集团找出运费最省的方案（甲、乙、丙三种车辆均要参与运送）．
