题目内容
【题目】已知:等边△ABC的边长为2,点D为平面内一点,且BD= ![]() AD=2
AD=2 ![]() ,则CD= .
,则CD= .
【答案】2或4
【解析】解:如图1:
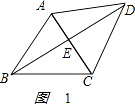
由BD= ![]() AD=2
AD=2 ![]() ,得
,得
AD=AB=AC=2.
由等腰三角形的性质,得
DE= ![]() .
.
sin∠DAE= ![]() ,
,
∠DAE=60°,△ACD是等边三角形,
CD=AC=2;
如图2:
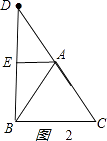 ,
,
由BD= ![]() AD=2
AD=2 ![]() ,得
,得
AD=AB=AC=2.
由等边三角形的性质,得
DE= ![]() ,∠DAE=∠BAE.
,∠DAE=∠BAE.
sin∠DAE= ![]() ,
,
∠DAE=∠BAE=60°,
AD与AC在同一条直线上,
CD=AC=2;
CD=AD+AC=2+2=4.
所以答案是:2或4.
【考点精析】本题主要考查了等腰三角形的性质和特殊角的三角函数值的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”才能正确解答此题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
【题目】七年级320名学生参加安全知识竞赛活动,小明随机调查了部分学生的成绩(分数为整数),绘制了频率分布表和频数分布直方图(不完整),请结合图表信息回答下列问题:
成绩(分) | 频数 |
71≤x<76 | 2 |
76≤x<81 | 8 |
81≤x<86 | 12 |
86≤x<91 | 10 |
91≤x<96 | 6 |
96≤x<101 | 2 |

(1)补全频数直方图;
(2)小明调查的学生人数是_______;频率分布表的组距是_______;
(3)七年级参加本次竞赛活动,分数![]() 在
在![]() 范围内的学生约有多少人.
范围内的学生约有多少人.




