题目内容
【题目】如图,△ABC是等边三角形,AN=BM,BN,MC相交于O,CH⊥BN于点H,求证:2OH=OC.

【答案】证明见解析.
【解析】
已知△ABC是等边三角形,根据等边三角形的性质可得AB=BC=AC,且三内角为60°,再由AN=BM,利用SAS得到△BAN≌△CBM,利用全等三角形的对应角相等及三角形外角的性质得到∠NOC=60°,在Rt△OHC中,利用30°角所对的直角边等于斜边的一半即可得2OH=OC.
∵△ABC为等边三角形,
∴AB=BC=AC,∠A=∠ABC=∠ACB=60°,
在△BAN和△CBM中,
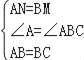 ,
,
∴△BAN≌△CBM(SAS),
∴∠ABN=∠BCM,
∵∠ABN+∠OBC=60°,
∴∠BCM+∠OBC=60°,
∵∠NOC为△OBC的外角,
∴∠NOC=∠BCM+∠OBC=60°,
在Rt△OHC,∠HCO=30°,
则2OH=OC.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目




