题目内容
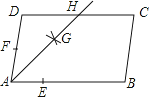
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=3EQ;④△PBF是等边三角形,其中正确的是( )
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=3EQ;④△PBF是等边三角形,其中正确的是( )

A. ①②③ B. ②③④ C. ①②④ D. ①③④
【答案】D
【解析】
求出BE=2AE,根据翻折的性质可得PE=BE,由此得出∠APE=30°,然后求出∠AEP=60°,再根据翻折的性质求出∠BEF=60°,根据直角三角形两锐角互余求出∠EFB=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半可得EF=2BE,判断出①正确;利用30°角的正切值求出PF=![]() PE,判断出②错误;求出BE=2EQ,EF=2BE,然后求出FQ=3EQ,判断出③正确;求出∠PBF=∠PFB=60°,然后得到△PBF是等边三角形,故④正确.
PE,判断出②错误;求出BE=2EQ,EF=2BE,然后求出FQ=3EQ,判断出③正确;求出∠PBF=∠PFB=60°,然后得到△PBF是等边三角形,故④正确.
∵AE=![]() AB,∴BE=2AE,
AB,∴BE=2AE,
由翻折的性质得:PE=BE,∴∠APE=30°,∴∠AEP=90°﹣30°=60°,∴∠BEF=![]() (180°﹣∠AEP)=
(180°﹣∠AEP)=![]() (180°﹣60°)=60°,∴∠EFB=90°﹣60°=30°,∴EF=2BE,故①正确;
(180°﹣60°)=60°,∴∠EFB=90°﹣60°=30°,∴EF=2BE,故①正确;
∵BE=PE,∴EF=2PE,
∵EF>PF,∴PF<2PE,故②错误;
由翻折可知EF⊥PB,∴∠EBQ=∠EFB=30°,∴BE=2EQ,EF=2BE,∴FQ=3EQ,故③正确;
由翻折的性质,∠EFB=∠EFP=30°,
则∠BFP=30°+30°=60°,
∵∠PBF=90°﹣∠EBQ=90°﹣30°=60°,∴∠PBF=∠PFB=60°,∴△PBF是等边三角形,故④正确.
故选D.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目