Question

【题目】如图，点B、E、F、C在一条直线上，AB=DE=10，AC=DF，BE=CF=CE．

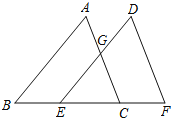
（1）求证：AB∥DE；

（2）求EG的长．

Answer 1

【答案】（1）详见解析；（2）5

【解析】

（1）由BE=CF，利用等式的性质得到BC=EF，利用SSS得到三角形ABC与三角形DEF全等，利用全等三角形对应角相等得到一对同位角相等，利用同位角相等两直线平行即可得证；

（2）由BE=CE得到E为BC中点，再由GE与AB平行，得到GE为中位线，利用中位线定理得到AB=2EG，即可求出EG的长．

解：（1）∵BE=CF，

∴BE+EC=CF+EC，即BC=EF，

在△ABC和△DEF中，

，

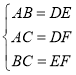∴△ABC≌△DEF（SSS），

∴∠B=∠DEF，

∴AB∥DE；

（2）∵GE∥AB，E为BC中点，

∴G为AC中点，即GE为△ABC的中位线，

∴EG=AB=5．