Question

【题目】对于三个数、、，用表示这三个数的中位数，用表示这三个数中最大数，例如：，，.

解决问题：

（1）填空： ，如果，则的取值范围为 ；

（2）如果，求的值；

（3）如果，求的值.

Answer 1

【答案】（1），；（2）﹣3或0；（3） x=3或﹣3．

【解析】析：（1）根据定义写出sin45°，cos60°，tan60°的值，确定其中位数；根据max{a，b，c}表示这三个数中最大数，对于max{3，53x，2x6}＝3，可得不等式组：则，可得结论；

（2）根据新定义和已知分情况讨论：①2最大时，x＋4≤2时，②2是中间的数时，x＋2≤2≤x＋4，③2最小时，x＋2≥2，分别解出即可；

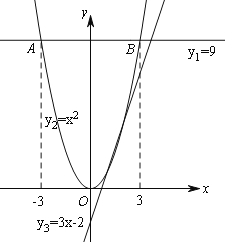
（3）不妨设y1＝9，y2＝x2，y3＝3x2，画出图象，根据M{9，x2，3x2}＝max{9，x2，3x2}，可知：三个函数的中间的值与最大值相等，即有两个函数相交时对应的x的值符合条件，结合图象可得结论．

（1）∵sin45°=，cos60°=，tan60°=，

∴M{sin45°，cos60°，tan60°}=，

∵max{3，5﹣3x，2x﹣6}=3，

则，

∴x的取值范围为：，

故答案为：，；

（2）2M{2，x+2，x+4}=max{2，x+2，x+4}，

分三种情况：①当x+4≤2时，即x≤﹣2，

原等式变为：2（x+4）=2，x=﹣3，

②x+2≤2≤x+4时，即﹣2≤x≤0，

原等式变为：2×2=x+4，x=0，

③当x+2≥2时，即x≥0，

原等式变为：2（x+2）=x+4，x=0，

综上所述，x的值为﹣3或0；

（3）不妨设y1=9，y2=x2，y3=3x﹣2，画出图象，如图所示：

结合图象，不难得出，在图象中的交点A、B点时，满足条件且M{9，x2，3x﹣2}=max{9，x2，3x﹣2}=yA=yB，

此时x2=9，解得x=3或﹣3．