题目内容
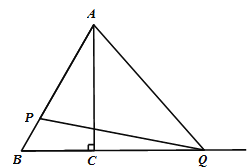
【题目】如图,在平面直角坐标系中,原点为O,点A(0,3),B(2,3),C(2,-3),D(0,-3).点P,Q是长方形ABCD边上的两个动点,BC交x轴于点M.点P从点O出发以每秒1个单位长度沿O→A→B→M的路线做匀速运动,同时点Q也从点O出发以每秒2个单位长度沿O→D→C→M的路线做匀速运动.当点Q运动到点M时,两动点均停止运动.设运动的时间为t秒,四边形OPMQ的面积为S.
(1)当t=2时,求S的值;
(2)若S<5时,求t的取值范围.
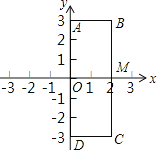
【答案】(1)S=5;(2)1.5<t<2或3<t<4
【解析】试题分析:设![]() 的面积为
的面积为![]()
![]() 的面积为则
的面积为则![]()
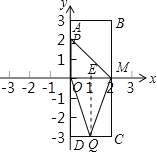
![]() 当t=2时,点P(0,2),Q(1,3),过点Q作QE⊥x轴于点
当t=2时,点P(0,2),Q(1,3),过点Q作QE⊥x轴于点![]() .根据三角形的面积公式分别求出
.根据三角形的面积公式分别求出![]()
![]() 进而得出
进而得出![]() 的值;
的值;
![]() 设点
设点![]() 运动的路程为
运动的路程为![]() 则点
则点![]() 运动的路程为
运动的路程为![]() 分五种情况进行讨论:①
分五种情况进行讨论:①![]() ;②
;②![]() ③
③![]() ④
④![]() ⑤
⑤![]() 针对每一种情况,首先确定出对应范围内点
针对每一种情况,首先确定出对应范围内点![]() 的位置,再根据三角形的面积公式求解即可.
的位置,再根据三角形的面积公式求解即可.
试题解析:设![]() 的面积为
的面积为![]()
![]() 的面积为
的面积为![]() 则
则![]()
(1)当t=2时,点P(0,2),Q(1,3),过点Q作QE⊥x轴于点![]() .
.
![]()
![]()
![]()
(2)设点P运动的路程为t,则点Q运动的路程为2t.
①当![]() 时,点P在线段OA上,点Q在线段OD上,
时,点P在线段OA上,点Q在线段OD上,
此时四边形OPMQ不存在,不合题意,舍去.
②当![]() 时,点P在线段OA上,点Q在线段DC上,
时,点P在线段OA上,点Q在线段DC上,
![]()
∵S<5,
∴t+3<5,解得t<2.
此时1.5<t<2.
③当![]() 时,点P在线段OA上,点Q在线段CM上,
时,点P在线段OA上,点Q在线段CM上,
![]()
∵S<5,
∴8t<5,解得t>3.
④当3<t<4时,点P在线段AB上,点Q在线段CM上,
![]()
∵S<5,
∴112t<5,解得t>3.
此时3<t<4.
⑤当t=4时,点P是线段AB的中点,点Q与M重合,两动点均停止运动,
此时四边形OPMQ不存在,不合题意,舍去.
综上所述,当S<5时,1.5<t<2或3<t<4.