题目内容
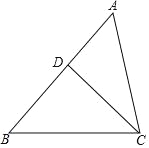
【题目】如图，△ABC中，CD是AB边上的高，AC=8，∠ACD=30°，tan∠ACB=
，点P为CD上一动点，当BP+
CP最小时，DP= ．
【答案】5
．
【解析】
试题分析：如图，作PE⊥AC于E，BE′⊥AC于E′交CD于P′．
∵CD⊥AB，∠ACD=30°，∠PEC=90°，AC=8，
∴PE=
PC，∠A=60°，∠ABE′=30°，AD=4，CD=4
，
∴PB+
PC=PB+PE，
∴当BE′⊥AC时，PB+PE=BP′+P′E′=BE′最小，
∵tan∠ACB=
=
，设BE′=5，CE′=3k，
∴AE′=8﹣3k，AB=16﹣6k，BD=16﹣6k﹣4=12﹣6k，
∴BC2=BD2+CD2=BE′2+CE′2，
∴（12﹣6k）2+48=9k2+75k2，
整理得k2+3k﹣4=0，
∴k=1或﹣4（舍弃），
∴BE′=5，
∴PB+
PC的最小值为5．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
【题目】体育课上全班男生进行了百米测试，达标成绩为14秒，下面是第一小组8名男生的成绩记录，其中“+”表示成绩大于14秒，“﹣”表示成绩小于14秒
﹣1 | +0.8 | 0 | ﹣1.2 | ﹣0.1 | 0 | +0.5 | ﹣0.6 |
（1）求这个小组的男生达标率是多少？
（2）求这个小组8名男生的平均成绩是多少？
