题目内容
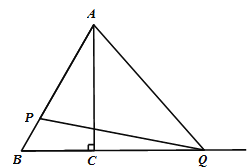
【题目】如图,在△ABC中,∠ACB=90°, ∠ABC=60°,BC=6.动点P从点A出发沿AB方向以每秒2个单位的速度运动,同时动点Q从点C出发沿射线BC方向以每秒2个单位的速度运动,当点P到达点B时,P、Q同时停止运动,连结PQ、QA.设点P运动的时间为t秒.
(1)当CQ=2BP时,求t的值;
(2)当t为何值时QP=QA;
(3)若线段PQ的中垂线与线段BC相交(包括线段的端点),则t的取值范围是 .(直接写出答案)
【答案】(1)4;(2)4.5;(3)1.5≤t≤3
【解析】试题分析:(1)根据直角三角形的性质求出AB,根据题意列出方程,解方程即可;
(2)根据相似三角形的性质求出PE、BE,根据勾股定理列方程,解方程求出t;
(3)根据线段垂直平分线的性质、勾股定理列式计算.
试题解析:解:(1)∵∠ACB=90°,∠ABC=60°,∴∠BAC=30°,∴AB=2BC=12,AC=![]() ,由题意得,CQ=2t,BP=12﹣2t,则2t=2(12﹣2t),得t=4;
,由题意得,CQ=2t,BP=12﹣2t,则2t=2(12﹣2t),得t=4;
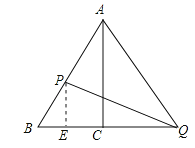
(2)作PE⊥BQ于E,则PE∥AC,∴△BPE∽△BAC,∴ ![]() ,解得,PE=
,解得,PE= ![]() ,BE=6﹣t,则EQ=EC+CQ=3t,∴PQ2=3(6﹣t)2+9t2,∵∠ACQ=90°,∴AQ2=AC2+CQ2=108+4t2,由题意得,108+4t2=3(6﹣t)2+9t2,解得,t=4.5;
,BE=6﹣t,则EQ=EC+CQ=3t,∴PQ2=3(6﹣t)2+9t2,∵∠ACQ=90°,∴AQ2=AC2+CQ2=108+4t2,由题意得,108+4t2=3(6﹣t)2+9t2,解得,t=4.5;
(3)当BP=BQ时,12﹣2t=6+2t,解得,t=1.5,当CP=CQ时,3(6﹣t)2+t2=(2t)2,解得,t=3,则当1.5≤t≤3时,线段PQ的中垂线与线段BC相交,故答案为:1.5≤t≤3.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目