Question

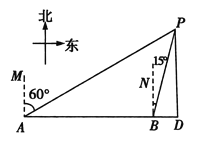
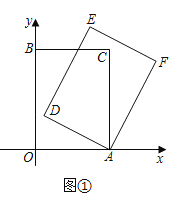
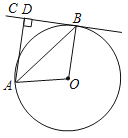
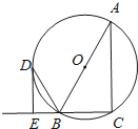
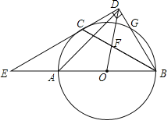
【题目】如图，AB为⊙O的直径，C，G是⊙O上两点，且弧AC＝弧CG，过点C的直线CD⊥BG于点D，交BA的延长线于点E，连接BC，交OD于点F．

（1）求证：CD是⊙O的切线；

（2）若，求AD的长．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）连接OC，AC，CG，根据圆周角定理可证出∠ABC＝∠CBG，由已知条件推出OC∥BG，根据两直线平行，同位角相等可得结果；

（2）根据平行证明△OCF∽△BDF，△EOC∽△EBD，可推出∠E＝30°，过A作AH⊥DE于H，可得∠CBD＝∠EBD＝30°，求出AH和DH即可求解．

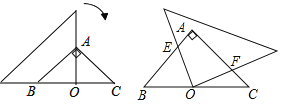
（1）证明：如图1，连接OC，AC，CG，

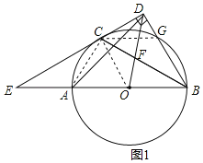
∵弧AC与弧CG相等，

∴∠ABC＝∠CBG，

∵OC＝OB，

∴∠OCB＝∠OBC，

∴∠OCB＝∠CBG，

∴OC∥BG，

∵CD⊥BG，

∴OC⊥CD，

∴CD是⊙O的切线；

（2）由图1：∵OC∥BD，∴△OCF∽△BDF，△EOC∽△EBD，

∴，∴，

∵OA＝OB，∴AE＝OA＝OB，

∴OC＝OE，∵∠ECO＝90°，∴∠E＝30°，

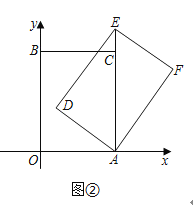
如图2，过A作AH⊥DE于H，

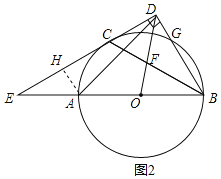
∵∠E＝30°

∴∠EBD＝60°，

∴∠CBD＝∠EBD＝30°，

∵CD＝，

∴BD＝3，DE＝3，BE＝6，

∴AE＝BE＝2，∴AH＝1，

∴EH＝，∴DH＝2，

∴在Rt△DAH中，AD＝．