题目内容
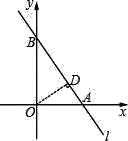
【题目】如图,已知一次函数 y=![]() x﹣3 与反比例函数 y=
x﹣3 与反比例函数 y=![]() 的图象相交于点 A(4,n),与 x 轴相交于点 B.
的图象相交于点 A(4,n),与 x 轴相交于点 B.
(1)求 n 与 k 的值;
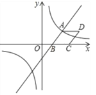
(2)以 AB 为边作菱形 ABCD,使点 C 在 x 轴正半轴上,点 D 在第一象限,求点 D 的坐标;
(3)观察反比例函数y=![]() 的图象,当 y>﹣2 时,请直接写出自变量 x 的取值范围.
的图象,当 y>﹣2 时,请直接写出自变量 x 的取值范围.
【答案】(1)n=3,k=12;(2)D(4+![]() ,3);(3) x<﹣6 或 x>0.
,3);(3) x<﹣6 或 x>0.
【解析】
(1)因为点![]() 在一次函数y=
在一次函数y=![]() x﹣3 的图象上,所以
x﹣3 的图象上,所以![]() ,又因为点
,又因为点![]() 在反比例函数
在反比例函数![]() 图象上,所以k=12.
图象上,所以k=12.
(2)首先根据直线方程求出点B的坐标,再由勾股定理求出菱形边长,再由菱形性质得知四边相等,最后根据平移性质的关系即可写出点![]() 的坐标.
的坐标.
(3)根据反比函数的性质即可得到当y>-2时,自变量x的取值范围.
解:(1)把 A 点坐标代入一次函数解析式可得 n=![]() ×4﹣3=3,
×4﹣3=3,
∴A(4,3),
∵A 点在反比例函数图象上,
∴k=3×4=12;
(2)在 y=![]() x﹣3 中,令 y=0 可得 x=2,
x﹣3 中,令 y=0 可得 x=2,
∴B(2,0),
∵A(4,3),
∴AB=![]() ,
,
∵四边形 ABCD 为菱形,且点 C 在 x 轴正半轴上,点 D 在第一象限,
∴BC=AB=![]() ,
,
∴点 C 由点 B 向右平移![]() 个单位得到,
个单位得到,
∴点 D 由点 A 向右平移![]() 个单位得到,
个单位得到,
∴D(4+![]() ,3);
,3);
(3)由(1)可知反比例函数解析式为 y=![]() , 令 y=﹣2 可得 x=﹣6,
, 令 y=﹣2 可得 x=﹣6,
结合图象可知当 y>﹣2 时,x 的取值范围为 x<﹣6 或 x>0.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目