��Ŀ����
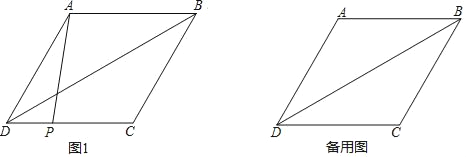
����Ŀ��������С����Ƶ�����������һ��������һ���㣬ʹ���������ε��������㹹�ɵ���������ԭ�������������ij߹���ͼ���̣�
��֪����ABC��
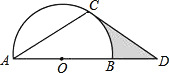
��������BC��������һ��P��ʹ����PAC�ס�ABC��
��������ͼ��
�����߶�AC�Ĵ�ֱƽ����GH��
�����߶�AB�Ĵ�ֱƽ����EF����GH�ڵ�O��
���Ե�OΪԲ�ģ���OAΪ�뾶��Բ��
���Ե�CΪԲ�ģ�CAΪ�뾶����������O�ڵ�D�����A���غϣ���
�������߶�AD��BC�ڵ�P��
���Ե�P�����������ĵ㣮
����С����Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ���������ͼ�ۼ���
��2����������֤����
֤������CD��AC��
��![]() ���� ����
���� ����
����� �������� ����
�֡ߡ��� �������� ����
���PAC�ס�ABC���� �����������������ݣ���

���𰸡���1������������2��![]() ��CAP��ABC��ACP��BCA��������Ƕ�Ӧ��ȵ���������������
��CAP��ABC��ACP��BCA��������Ƕ�Ӧ��ȵ���������������
��������
(1)������Ŀ����������⼴�ɣ�
(2)����CD������ͼ֪��AC��CD��,�ɵá�CAP����ABC������ACP����BCA��
�ɵ���ACP�ס�BCA��������Ƕ�Ӧ��ȵ��������������ƣ�.
�⣺��1����ȫͼ����ͼ��ʾ��

��2������CD������ͼ֪��AC��CD��
��![]() =
=![]() ��
��
���CAP����ABC��
�ߡ�ACP����BCA��
���ACP�ס�BCA��������Ƕ�Ӧ��ȵ��������������ƣ���
�ʴ�Ϊ��![]() ��CAP��ABC��ACP��BCA��������Ƕ�Ӧ��ȵ��������������ƣ�
��CAP��ABC��ACP��BCA��������Ƕ�Ӧ��ȵ��������������ƣ�

 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�