题目内容
【题目】如图,在矩形ABCD中,AB=6,BC=8,沿直线MN对折,使A、C重合,直线MN交AC于O.
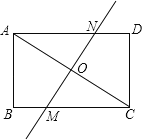
(1)求证:△COM∽△CBA;
(2)求线段OM的长度.
【答案】(1)证明见解析(2)![]()
【解析】解:(1)证明:∵A与C关于直线MN对称,∴AC⊥MN。∴∠COM=90°。
在矩形ABCD中,∠B=90°,∴∠COM=∠B。
又∵∠ACB=∠ACB,∴△COM∽△CBA。
(2)∵在Rt△CBA中,AB=6,BC=8,∴由勾股定理得AC=10。∴OC=5。
∵△COM∽△CBA,∴![]() ,即
,即![]() 。∴OM=
。∴OM=![]() 。
。
(1)根据A与C关于直线MN对称得到AC⊥MN,进一步得到∠COM=90°,从而得到在矩形ABCD中∠COM=∠B,最后证得△COM∽△CBA;
(2)利用(1)的相似三角形的对应边成比例得到比例式后即可求得OM的长。

练习册系列答案
相关题目