题目内容
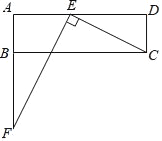
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,
![]()
(1)写出数轴上点B表示的数 ;
(2)|5-3|表示5与3之差的绝对值,实际上也可理解为5与3两数在数轴上所对的两点之间的距离.如![]() 的几何意义是数轴上表示有理数
的几何意义是数轴上表示有理数![]() 的点与表示有理数3的点之间的距离.试探索:
的点与表示有理数3的点之间的距离.试探索:
①:若![]() ,则
,则![]() = .②:
= .②:![]() 的最小值为 .
的最小值为 .
(3)动点P从O点出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为(>0)秒.
①:当=1时,A,P两点之间的距离为 ;②:当= 时,A,P之间的距离为2.
(4)动点P,Q分别从O,B两点,同时出发,点P以每秒4个单位长度沿数轴向右匀速运动,Q点以P点速度的两倍,沿数轴向右匀速运动,设运动时间为t(t>0)秒.当t= ,P,Q之间的距离为4.
【答案】(1)![]() ;(2)①6或10;②20;(3)①6,②3或5;④2或4.
;(2)①6或10;②20;(3)①6,②3或5;④2或4.
【解析】
(1)根据两点间的距离公式可得数轴上点B表示的数;
(2)①根据绝对值的性质即可求解;
②根据两点间的距离公式即可求解;
(3)设经过t秒时,A,P之间的距离为2,根据距离的等量关系即可求解;
(4)设经过t秒时,P,Q之间的距离为4,根据距离的等量关系即可求解.
解:(1)点B表示的数8-20=-12.
故答案为:-12;
(2)①|x-8|=2,
x-8=±2,
则x=6或10.
故答案为:6或10;
②|x+12|+|x-8|的最小值为8-(-12)=20.
故答案为:20;
(3)设经过t秒时,A,P之间的距离为2.此时P点表示的数是5t,
则|8-5t|=2,
解得t=2或t= ![]() .
.
故当t为2或![]() 秒时,A,P两点之间的距离为2;
秒时,A,P两点之间的距离为2;
(4)设经过t秒时,P,Q之间的距离为4.
此时P点表示的数是5t,Q点表示的数-12+10t,
则|-12+10t-5t|=4
解得t=![]() 或t=
或t= ![]() .
.
故当t为![]() 或
或![]() 秒时,P,Q之间的距离为4.
秒时,P,Q之间的距离为4.