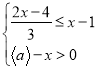题目内容
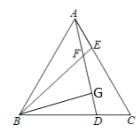
【题目】如图,△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F,BG⊥AD,垂足为G.
(1)求证:AD=BE;
(2)求∠AFB的度数;
(3)线段FG与BF有什么数量关系?请说明理由.
【答案】(1)见解析(2)120°(3)见解析
【解析】
(1)利用等边三角形的性质得到一对边相等,一对角相等,再根据已知边相等,利用SAS得到三角形全等,利用全等三角形的对应边相等即可得证;
(2)利用全等三角形对应角相等得到一对角相等,再利用外角性质及等边三角形的性质求出∠BFG的度数,从而可得结论;
(3)根据“30°角所对直角边等于斜边的一半”可得结论.
(1)证明:∵△ABC为等边三角形,
∴AB=AC,∠BAE=∠ACB=60°,
∵AE=CD,
∴△ABE≌△CAD(SAS),
∴AD=BE;
(2)解:∵△ABE≌△CAD,
∴∠ABE=∠CAD,
∵∠BAE=∠CAD+∠BAD,
∴∠ABE+∠BAD=60°,
∵∠BFD是△ABF的外角,
∴∠BFD=∠ABE+∠BAD=60°.
∴∠AFB=120°
(3)FG=![]() BF
BF
由(2)可知∠BFG=60°
∵BG⊥AD
∴∠FBG=30°,
∴FG=![]() BF
BF

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目