题目内容
【题目】如图,某大楼的顶部树有一块广告牌CD,小明在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度 ![]() ,AB=10米,AE=15米.
,AB=10米,AE=15米.
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据: ![]() )
)
【答案】
(1)解:
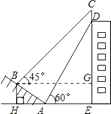
过B作BG⊥DE于G,Rt△ABF中,i=tan∠BAH= ![]()
∴∠BAH=30°,∴BH= ![]() AB=5;
AB=5;
(2)解:由(1)得:BH=5,AH=5 ![]() ,∴BG=AH+AE=5
,∴BG=AH+AE=5 ![]() +15,
+15,
Rt△BGC中,∠CBG=45°,∴CG=BG=5 ![]() +15.
+15.
Rt△ADE中,∠DAE=60°,AE=15,∴DE= ![]() AE=15
AE=15 ![]() .
.
∴CD=CG+GE﹣DE=5 ![]() +15+5﹣15
+15+5﹣15 ![]() =20﹣10
=20﹣10 ![]() ≈2.7m.
≈2.7m.
答:宣传牌CD高约2.7米.
【解析】(1)由i=tan∠BAH的值,求出BH的值;(2)由(1)得到BH,AH ,BG=AH+AE的值,Rt△BGC中,∠CBG=45°,得到CG=BG的值;在Rt△ADE中,由∠DAE=60°,AE的值,求出DE、AE的值,得到CD=CG+GE﹣DE的值,即宣传牌CD的高.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目