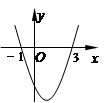题目内容
(10分) 如图,已知抛物线y = ax2-x + c经过点Q(-2,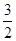 ),且它的顶点P的横坐标为-1.设抛物线与x轴相交于A、B两点。
),且它的顶点P的横坐标为-1.设抛物线与x轴相交于A、B两点。

(1)求抛物线的解析式及顶点P的坐标;
(2)求A、B两点的坐标;并求当x为何值时,y>0?
(3)设PB交y轴于C点,求线段PC的长。
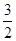 ),且它的顶点P的横坐标为-1.设抛物线与x轴相交于A、B两点。
),且它的顶点P的横坐标为-1.设抛物线与x轴相交于A、B两点。
(1)求抛物线的解析式及顶点P的坐标;
(2)求A、B两点的坐标;并求当x为何值时,y>0?
(3)设PB交y轴于C点,求线段PC的长。
(1)y =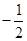 x2-x+
x2-x+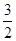 (3分) P(-1,2) (1分)
(3分) P(-1,2) (1分)
(2)A(-3,0) B(1,0) -3<x<1 (3分)
(3)C(0,1) PC=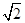 (3分)
(3分)
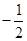 x2-x+
x2-x+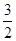 (3分) P(-1,2) (1分)
(3分) P(-1,2) (1分)(2)A(-3,0) B(1,0) -3<x<1 (3分)
(3)C(0,1) PC=
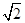 (3分)
(3分)试题分析:解:
解:
(1)由题意分析,则有抛物线y = ax2-x + c的顶点式是
X=
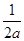 =-1
=-1所以
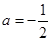
把各点代入,得出
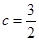
故:y =
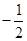 x2-x+
x2-x+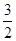 P(-1,2)
P(-1,2) (2)y=0
所以A(-3,0) B(1,0)
故在 -3<x<1 时y>0
(3)设经过P,B的直线是
Y=ax+b
代入: P(-1,2) B(1,0) 得出:y=-x+1
所以C(0,1)
故PC=
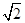
点评:此类试题的解答较麻烦,考生首先要把式子化简求出解析式,进而和各个轴的交点进行分析比较

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
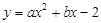 经过(2,1)和(6,-5)两点.
经过(2,1)和(6,-5)两点.
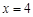 右侧的此抛物线上一点,过点P作PM
右侧的此抛物线上一点,过点P作PM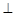
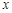 轴,垂足为M. 若以A、P、M为顶点的三角形与△OCB相似,求点P的坐标;
轴,垂足为M. 若以A、P、M为顶点的三角形与△OCB相似,求点P的坐标; 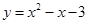 经过点
经过点 、
、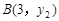 ,则
,则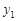 与
与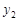 的大小关系是_______.
的大小关系是_______.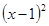 +3向右平移2个单位后,得到的新抛物线解析式是 .
+3向右平移2个单位后,得到的新抛物线解析式是 .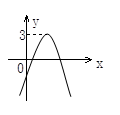
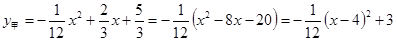 、
、 ,那么在这次比赛中,成绩较好的学生是( )
,那么在这次比赛中,成绩较好的学生是( )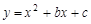 与
与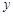 轴交于点
轴交于点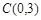 ,与
,与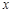 轴交于
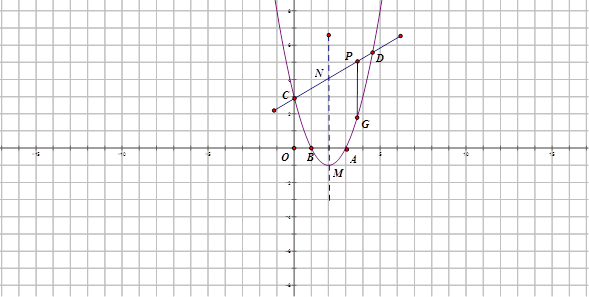
轴交于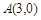 ,B两点(点A在点B的右侧),过C作直线
,B两点(点A在点B的右侧),过C作直线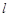 ,与抛物线相交于点
,与抛物线相交于点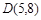 ,与对称轴交于点N,点
,与对称轴交于点N,点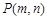 为直线
为直线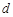
 <5时,请用含
<5时,请用含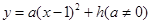 与
与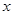 轴交于A(
轴交于A(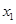 ,0)、B(3,0)两点,则
,0)、B(3,0)两点,则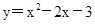 ,当
,当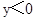 时自变量x的取值范围是 。
时自变量x的取值范围是 。