题目内容
将抛物线y=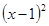 +3向右平移2个单位后,得到的新抛物线解析式是 .
+3向右平移2个单位后,得到的新抛物线解析式是 .
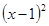 +3向右平移2个单位后,得到的新抛物线解析式是 .
+3向右平移2个单位后,得到的新抛物线解析式是 .y=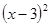 +3
+3
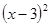 +3
+3试题分析:抛物线的平移规律:左加右减,上加下减.
将抛物线y=
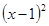 +3向右平移2个单位后,得到的新抛物线解析式是y=
+3向右平移2个单位后,得到的新抛物线解析式是y=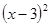 +3.
+3.点评:本题属于基础应用题,只需学生熟练掌握抛物线的平移规律,即可完成.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
题目内容
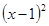 +3向右平移2个单位后,得到的新抛物线解析式是 .
+3向右平移2个单位后,得到的新抛物线解析式是 .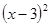 +3
+3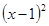 +3向右平移2个单位后,得到的新抛物线解析式是y=
+3向右平移2个单位后,得到的新抛物线解析式是y=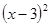 +3.
+3.
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案