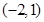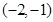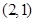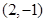题目内容
(8分)如图,抛物线 与
与 轴交于点
轴交于点 ,与
,与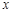 轴交于
轴交于 ,B两点(点A在点B的右侧),过C作直线
,B两点(点A在点B的右侧),过C作直线 ,与抛物线相交于点
,与抛物线相交于点 ,与对称轴交于点N,点
,与对称轴交于点N,点 为直线
为直线 上的一个动点,过P作
上的一个动点,过P作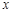 轴的垂线交抛物线于点G,设线段PG的长度为
轴的垂线交抛物线于点G,设线段PG的长度为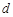

(1)求该抛物线的函数解析式
(2)当0< <5时,请用含
<5时,请用含 的代数式表示
的代数式表示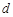 ,求出
,求出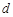 的最大值
的最大值
(3)是否存在这样的点P,使以M,N,P,G为顶点的四边形是平行四边形,若存在,请求出点P的坐标;若存在,请说明理由。
 与
与 轴交于点
轴交于点 ,与
,与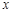 轴交于
轴交于 ,B两点(点A在点B的右侧),过C作直线
,B两点(点A在点B的右侧),过C作直线 ,与抛物线相交于点
,与抛物线相交于点 ,与对称轴交于点N,点
,与对称轴交于点N,点 为直线
为直线 上的一个动点,过P作
上的一个动点,过P作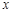 轴的垂线交抛物线于点G,设线段PG的长度为
轴的垂线交抛物线于点G,设线段PG的长度为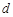

(1)求该抛物线的函数解析式
(2)当0<
 <5时,请用含
<5时,请用含 的代数式表示
的代数式表示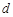 ,求出
,求出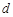 的最大值
的最大值(3)是否存在这样的点P,使以M,N,P,G为顶点的四边形是平行四边形,若存在,请求出点P的坐标;若存在,请说明理由。
(1)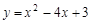 (2)
(2)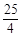 (3) P的坐标
(3) P的坐标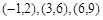
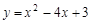 (2)
(2)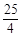 (3) P的坐标
(3) P的坐标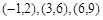
试题分析:
解:
(1)
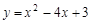
(2)直线
 :
: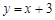 又
又 ∴
∴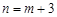

0<
 <5时
<5时 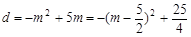
∴
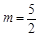 时,
时,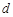 有最大值
有最大值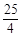
(1)顶点M(2,-1),N(2,5),则MN=6
∵PG∥MN ∴只要PG=MN=6就能证明四边形为平行四边形
当P在G的上面时
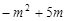 =6,解得
=6,解得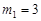 ,
,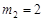 (舍去)
(舍去)当P在G的下面时-(
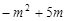 )=6解得
)=6解得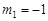 ,
,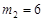 时
时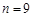
∴P的坐标
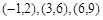
点评:此类试题的解答主要是分析二次函数的顶点公式,以及求法,几种做法。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 经过点(
经过点( ,
, ).
). 的值;
的值; ,
, ),用含
),用含 的式子分别表示
的式子分别表示 ,且对于任意的实数
,且对于任意的实数 ,都有
,都有 ≥
≥ ,直接写出
,直接写出 的取值范围.
的取值范围. ),且它的顶点P的横坐标为-1.设抛物线与x轴相交于A、B两点。
),且它的顶点P的横坐标为-1.设抛物线与x轴相交于A、B两点。


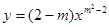 是二次函数,求m的值
是二次函数,求m的值 的对称轴是__________;
的对称轴是__________;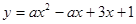 的图象与x轴有且只有一个交点,写出a所有可能的值____.
的图象与x轴有且只有一个交点,写出a所有可能的值____.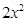 先向左平移2个单位,再向下平移1个单位得到一个新的抛物线,则新抛物线的顶点坐标是
先向左平移2个单位,再向下平移1个单位得到一个新的抛物线,则新抛物线的顶点坐标是