题目内容
【题目】如图，抛物线y＝ax2＋bx－3与x轴交于点A（1，0）和点B，与y轴交于点C，且其对称轴l为x＝－1，点P是抛物线上B，C之间的一个动点（点P不与点B，C重合）．
（1）直接写出抛物线的解析式；
（2）小唐探究点P的位置时发现：当动点N在对称轴l上时，存在PB⊥NB，且PB＝NB的关系，请求出点P的坐标；
（3）是否存在点P使得四边形PBAC的面积最大？若存在，请求出四边形PBAC面积的最大值；若不存在，请说明理由．
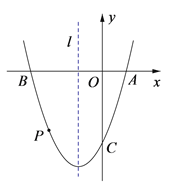
【答案】 （1）抛物线的解析式为y＝x2＋2x－3；
（2点P的坐标为（－1－
，－2）；
（3）存在，四边形PBAC的面积最大，最大值为
．
【解析】（1）由抛物线y=ax2+bx-3（a≠0）点A（1，0）和点B（-3，0），由待定系数法就可以直接求出a、b的值而求出抛物线的解析式．
（2）由（1）的解析式就可以求出C点的坐标，求出OC的值，在Rt△CON中由勾股定理就可以求出CN的值，CP1=NP1时，
作P1H⊥CN于H，由三角形相似就可以求出P1N的值，从而求出P1的坐标；
（3）设出点E的坐标，连接BE、CE，作EG⊥OB于点G，就可以表示EG、BG、OG的值就可以表示出四边形BOCE的面积，然后化为顶点式就可以求出其面积的最大值．
解：（1）抛物线的解析式为y＝x2＋2x－3．
（2）
如图，过点P作PM⊥x轴于点M，
设抛物线对称轴l交x轴于点Q．
∵PB⊥NB，∴∠PBN＝90°，
∴∠PBM＋∠NBQ＝90°．
∵∠PMB＝90°，
∴∠PBM＋∠BPM＝90°．
∴∠BPM＝∠NBQ．
又∵∠BMP＝∠BNQ＝90°，PB＝NB，
△BPM≌△NBQ．∴PM＝BQ．
∵抛物线y＝x2＋2x－3与x轴交于点A（1，0）和点B，且对称轴为x＝－1，
∴点B的坐标为（－3，0），点Q的坐标为（－1，0）．∴BQ＝2．∴PM＝BQ＝2．
∵点P是抛物线y＝x2＋2x－3上B、C之间的一个动点，
∴结合图象可知点P的纵坐标为－2．
将y＝－2代入y＝x2＋2x－3，得－2＝x2＋2x－3．
解得x1＝－1－，x2＝－1＋（舍去）．
∴此时点P的坐标为（－1－，－2）．
（3）存在．
如图，连接AC．可设点P的坐标为（x，y）（－3﹤x﹤0），
则y＝x2＋2x－3．∵点A（1，0），∴OA＝1．
∵点C是抛物线与y轴的交点，∴令x＝0，得y＝－3．即点C（0，－3）．
∴OC＝3．由（2）可知
S四边形PBAC＝S△BPM＋S四边形PMOC＋S△AOC
＝
BM·PM＋（PM＋OC）·OM＋OA·OC
＝（x＋3）（－y）＋（－y＋3）（－x）＋×1×3
＝－
y－
x＋．将y＝x2＋2x－3代入可得
S四边形PBAC＝－（x2＋2x－3）－x＋
＝－（x＋）2＋．∵－﹤0，－3﹤x﹤0，
∴当x＝－时，S四边形PBAC有最大值．
此时，y＝x2＋2x－3＝－
．
∴当点P的坐标为（－，－）时，
四边形PBAC的面积最大，最大值为．
“点睛”本题考查了二次函数的综合题：熟练掌握二次函数的性质和二次函数图象上点的坐标特征；会运用待定系数法求函数的解析式；能灵活运用相似三角形性质表示线段之间的关系；理解坐标与图形性质，会运用勾股定理的逆定理证明三角形为直角三角形；学会用分类讨论的思想解决数学问题.
