题目内容
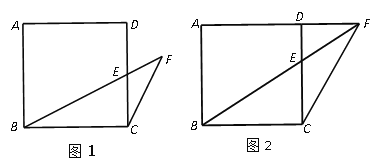
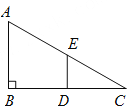
【题目】如图,在Rt△ABC中,∠B=90°,BC =2 AB = 8,点D,E分别是边BC,AC的中点,连接DE.将△EDC绕点C按顺时针方向旋转,当△EDC旋转到A,D,E三点共线时,线段BD的长为__.
【答案】4![]() 或
或![]()
【解析】分两种情况分析,A、D、E三点所在直线与BC不相交和与BC相交,然后利用勾股定理分别求解即可求得答案.
解:(3)①如图所示,
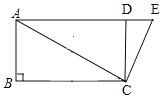
∵AC=4![]() ,CD=4,CD⊥AD,
,CD=4,CD⊥AD,
∴AD=![]() =
=![]() =
=![]() =8,
=8,
∵AD=BC,AB=CD,∠B=90°,
∴四边形ABCD是矩形,
∴BD=AC=4![]() .
.
②如图所示,连接BD,过点D作AC的垂线交AC于点Q,过点B作AC的垂线交AC于点P,
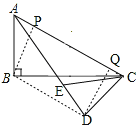
∵AC=4![]() ,CD=4,CD⊥AD,
,CD=4,CD⊥AD,
∴AD=![]() =
=![]() =
=![]() =8,
=8,
∵点D、E分别是边BC、AC的中点,
∴DE=![]() AB=
AB=![]() ×(8÷2)=
×(8÷2)=![]() ×4=2,
×4=2,
∴AE=AD-DE=8-2=6,
由(2),可得
![]() =
=![]() ,
,
∴BD=![]() =
=![]() .
.
综上所述,BD的长为4![]() 或
或![]() .
.
“点睛”此题主要考查了几何变换综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,要熟练掌握.还考查了线段长度的求法,以及矩形的判定和性质的应用,要熟练掌握.

练习册系列答案
相关题目