题目内容
如图，PA为⊙O的切线，A为切点，PO交⊙O于点B，PA=4，OA=3，则cos∠APO
的值为( )
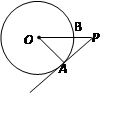
的值为( )
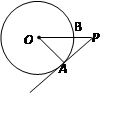
A． | B． | C． | D． |
C
根据切线的性质，△OAP是直角三角形，根据勾股定理就可以求出OP=5，则可以求得cos∠APO的值．
解：∵PA为⊙O的切线，A为切点，
∴OA⊥AP．
又PA=4，OA=3，∴OP=5．
∴cos∠APO=．
故本题选C．
本题运用了切线的性质定理，通过切线的性质定理得到△OAP是直角三角形，是解决本题的关键．
解：∵PA为⊙O的切线，A为切点，
∴OA⊥AP．
又PA=4，OA=3，∴OP=5．
∴cos∠APO=
．故本题选C．
本题运用了切线的性质定理，通过切线的性质定理得到△OAP是直角三角形，是解决本题的关键．
练习册系列答案
相关题目
，并说明理由；
A，与大圆相交于点B，大圆的弦BC⊥AB于点B，过点C作大圆的切线CD交AB的延长线于点D，连接OC交小圆于点E，连接BE、BO．
，扇形半径为R，则R与
，内切圆半径是
，则内切圆的面积与三角形面积之比是( )
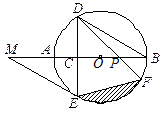
图，AB是⊙O的直径，弦DE垂直平分半径OA，C为垂足，DE＝3，
线于点M．
