题目内容
若一直角三角形的斜边长为 ,内切圆半径是
,内切圆半径是 ,则内切圆的面积与三角形面积之比是( )
,则内切圆的面积与三角形面积之比是( )
 ,内切圆半径是
,内切圆半径是 ,则内切圆的面积与三角形面积之比是( )
,则内切圆的面积与三角形面积之比是( )A. | B. | C. | D. |
B
连接内心和直角三角形的各个顶点,设直角三角形的两条直角边是a,b.则直角三角形的面积是 r;又直角三角形内切圆的半径r=
r;又直角三角形内切圆的半径r= ,则a+b=2r+c,所以直角三角形的面积是r(r+c);因为内切圆的面积是πr2,则它们的比是
,则a+b=2r+c,所以直角三角形的面积是r(r+c);因为内切圆的面积是πr2,则它们的比是 。
。
解:设直角三角形的两条直角边是a,b,则有:
S= r,又∵r=
r,又∵r= ,∴∴a+b=2r+c,
,∴∴a+b=2r+c,
将a+b=2r+c代入S = r得:S=
r得:S= r=r(r+c)
r=r(r+c)
又∵内切圆的面积是πr2,∴它们的比是 。
。
故答案选B 。
 r;又直角三角形内切圆的半径r=
r;又直角三角形内切圆的半径r= ,则a+b=2r+c,所以直角三角形的面积是r(r+c);因为内切圆的面积是πr2,则它们的比是
,则a+b=2r+c,所以直角三角形的面积是r(r+c);因为内切圆的面积是πr2,则它们的比是 。
。解:设直角三角形的两条直角边是a,b,则有:
S=
 r,又∵r=
r,又∵r= ,∴∴a+b=2r+c,
,∴∴a+b=2r+c,将a+b=2r+c代入S =
 r得:S=
r得:S= r=r(r+c)
r=r(r+c)又∵内切圆的面积是πr2,∴它们的比是
 。
。故答案选B 。

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
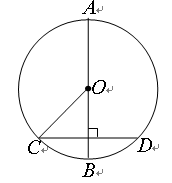
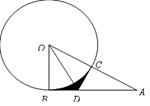
 为圆心,1为半径作
为圆心,1为半径作 .
.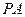 ,若
,若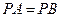 ,试判断
,试判断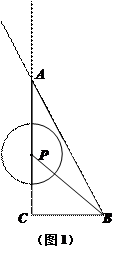
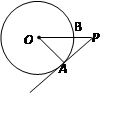




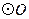 的切线,切点为
的切线,切点为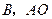 交
交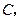 过点
过点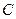 作
作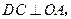 交
交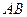 于点
于点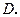
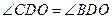 ;
;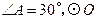 的半径为4,求CD的长;
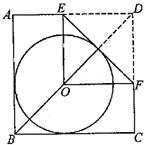
的半径为4,求CD的长;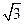 ,AC是⊙O的直径,AC⊥BD于F,∠A=30°.
,AC是⊙O的直径,AC⊥BD于F,∠A=30°.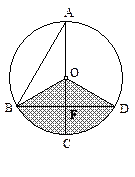


 .
.