题目内容
如图,在正方形铁皮上剪下一个圆和扇形(圆与扇形外切,且与正方形的边相切),
使之恰好围成如图所示的一个圆锥模型,设圆半径为 ,扇形半径为R,则R与
,扇形半径为R,则R与 的关系是 ( )
的关系是 ( )

使之恰好围成如图所示的一个圆锥模型,设圆半径为
 ,扇形半径为R,则R与
,扇形半径为R,则R与 的关系是 ( )
的关系是 ( )
| A.R=2r | B.R="4r" |
| C.R=2πr | D.R=4πr |
B
根据弧长公式分别计算出扇形的弧长=  =
=  πR,圆的周长=2πr;然后根据圆锥的侧面展开图为扇形,扇形的弧长等于圆锥底面圆的周长得到
πR,圆的周长=2πr;然后根据圆锥的侧面展开图为扇形,扇形的弧长等于圆锥底面圆的周长得到 πR=2πr,即可得到R与r的关系.
πR=2πr,即可得到R与r的关系.
解:∵扇形的弧长= =
= πR,
πR,
圆的周长=2πr,
∴ πR=2πr,
πR=2πr,
∴R=4r.
故选B.
本题考查了圆锥的计算:圆锥的侧面展开图为扇形,扇形的半径等于圆锥的母线长,扇形的弧长等于圆锥底面圆的周长.也考查了弧长的公式.
 =
=  πR,圆的周长=2πr;然后根据圆锥的侧面展开图为扇形,扇形的弧长等于圆锥底面圆的周长得到
πR,圆的周长=2πr;然后根据圆锥的侧面展开图为扇形,扇形的弧长等于圆锥底面圆的周长得到 πR=2πr,即可得到R与r的关系.
πR=2πr,即可得到R与r的关系.解:∵扇形的弧长=
 =
= πR,
πR,圆的周长=2πr,
∴
 πR=2πr,
πR=2πr,∴R=4r.
故选B.
本题考查了圆锥的计算:圆锥的侧面展开图为扇形,扇形的半径等于圆锥的母线长,扇形的弧长等于圆锥底面圆的周长.也考查了弧长的公式.

练习册系列答案
相关题目
 图2是某巷子的俯视图,巷子路面宽4 m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连
图2是某巷子的俯视图,巷子路面宽4 m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连 接EF,交CD于点G,若GF的长度至少能达到车身宽度,即车辆能通过.
接EF,交CD于点G,若GF的长度至少能达到车身宽度,即车辆能通过. 为半径的弧),长8m,宽3m的消防车就可以通过该弯道了,具体的方案如图3,其中OM⊥OM′,你能帮小平算出,ON至少为多少时,这种消防车可以通过该巷子,?
为半径的弧),长8m,宽3m的消防车就可以通过该弯道了,具体的方案如图3,其中OM⊥OM′,你能帮小平算出,ON至少为多少时,这种消防车可以通过该巷子,?
 ,
, ,则向量
,则向量 可表示为( ).
可表示为( ).




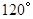 的扇形围成一个圆锥的侧面(接缝忽略不计),
的扇形围成一个圆锥的侧面(接缝忽略不计),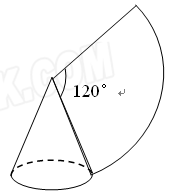

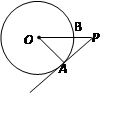




 为
为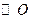 的切线,
的切线,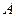 为切点,
为切点,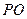 交
交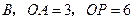 ,求
,求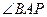 的度数.
的度数.
 中
中 ,
, 则⊙
则⊙
 线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作
线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作
