Question

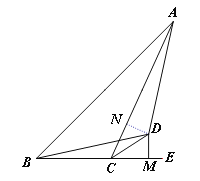
【题目】已知：如图，点B、C、E三点在同一条直线上，CD平分∠ACE，∠DBM=∠DAN，DM⊥BE于M，DN⊥AC于N.（1）求证：△BDM≌△ADN ；（2）若AC=2，BC=1，求CM的长.

Answer 1

【答案】（1）见解析；（2）0.5

【解析】试题分析：（1）根据HL易证Rt△DCN≌Rt△DCM，可得CN=CM，进而可以证明Rt△ADN≌Rt△BDM；

（2）由Rt△ADN≌Rt△BDM，可得AN=BM，变形得出答案即可．

试题解析：解：（1）∵CD平分∠ACE，DM⊥BE，DN⊥AC，∴DN=DM．

在Rt△DCN和Rt△DCM中，∵CD=CD，DN=DM，∴Rt△DCN≌Rt△DCM（HL），∴CN=CM，

在Rt△ADN和Rt△BDM中，∵∠DBM=∠DAN，∠AND=∠BMD，ND=DM，∴Rt△ADN≌Rt△BDM（AAS）；

(2)∵Rt△ADN≌Rt△BDM，∴AN=BM．∵AN=AC-CN， BM=BC+CM，∴AC-CN=BC+CM，

∴AC-CM=BC+CM，∴2CM=AC-BC．∵AC=2，BC=1，∴CM=0.5．