题目内容
【题目】如图,在△ABC中,∠ACB=90°,D为AB边上一点,连接CD,E为CD的中点,连接BE并延长至点F,使得EF=EB,连接DF交AC于点G,连接CF,
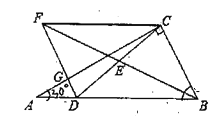
(1)求证:四边形DBCF是平行四边形
(2)若∠A=30°,BC=4,CF=6,求CD的长
【答案】(1)见解析(2)![]()
【解析】
(1)根据对角线互相平分即可证明;
(2)由四边形DBCF是平行四边形,可得CF∥AB,DF∥BC,可得∠FCG=∠A=30°,∠CGF=∠CGD=∠ACB=90°,由直角三角形的性质得到FG,CG,GD的长,由勾股定理即可求解.
(1)∵E为CD的中点,
∴CE=DE,又EF=EB
∴四边形DBCF是平行四边形
(2)∵四边形DBCF是平行四边形,∴CF∥AB,DF∥BC,
∴∠FCG=∠A=30°,∠CGF=∠CGD=∠ACB=90°,
在Rt△FCG中,CF=6,
∴FG=![]() CF=3,CG=3
CF=3,CG=3![]()
∵DF=BC=4,
∴DG=1,
∴在Rt△DCG中,CD=![]()

练习册系列答案
相关题目
【题目】求一个正数的算术平方根,有些数可以直接求得,如![]() ,有些数则不能直接求得,如
,有些数则不能直接求得,如![]() ,但可以通过计算器求得,还可以通过一组数的内在联系,运用规律求得.请同学们观察下表:
,但可以通过计算器求得,还可以通过一组数的内在联系,运用规律求得.请同学们观察下表:
| 16 | 0.16 | 0.0016 | 1600 | 160000 | … |
| 4 | 0.4 | 0.04 | 40 | 400 | … |
(1)表中所给的信息中,你能发现什么规律?(请将规律用文字表述出来)
(2)运用你发现的规律,探究下列问题:已知![]() ,求下列各数的算术平方根:
,求下列各数的算术平方根:
①0.0206;②2060000.