题目内容
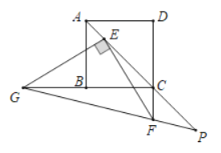
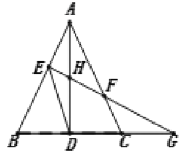
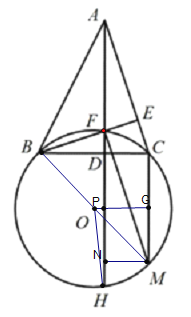
【题目】如图,在△ABC 中,AD⊥BC 于 D(其中 BD>CD),BE⊥AC 于 E,AD 与 BE 相交于点 F,直线 AD 与△BCF 的外接圆 O 交于点 H,点 M 在圆 O 上,满足弧 HM=弧 CF,连接 FM.
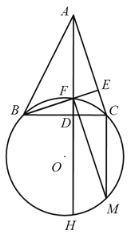
(1)求证:AF=CM;
(2)若∠ABE=45°,FH ![]() ,圆O的直径为
,圆O的直径为![]() ,求BF的值.
,求BF的值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据AD⊥BC,BE⊥AC得∠BDF=∠AEF=90°,再由![]() 得CM∥HF,证明四边形AFMC为平行四边形即可求证AF=CM;
得CM∥HF,证明四边形AFMC为平行四边形即可求证AF=CM;
(2)连接BM,过点O作OG⊥CM于点G,交AH于点P,过点M作MN⊥AH于点N,连接PH,先证BM为直径,设AF=5a,根据直径为![]() ,解出a的值,分别求出MN,FD的值,再根据△FBD∽△FNM,求出BF的值.
,解出a的值,分别求出MN,FD的值,再根据△FBD∽△FNM,求出BF的值.
(1)证明:∵AD⊥BC,BE⊥AC,
∴∠BDF=∠AEF=90°,
∵∠AFE=∠BFD(对顶角),
∴∠FBD=∠EAF,
∵∠FBC和∠CMF都是![]() 对应的圆周角,
对应的圆周角,
∴∠FBC=∠CMF,
∴∠EAF=∠CMF,
∵![]() ,
,
∴CM∥HF,
∴∠CMF=∠MFH,
∴∠MFH=∠EAF,
∴AC∥FM,
∴四边形AFMC为平行四边形,
∴AF=CM;
(2)连接BM,过点O作OG⊥CM于点G,交AH于点P,过点M作MN⊥AH于点N,连接PH,
∵AD⊥BC,CM∥AD,
∴CM⊥BC,
∴∠BCM=90°,
∴BM为直径,
设AF=5a,
∴CM=AF=5a,
∵OG⊥CM,
∴GM=![]() ,
,
∴OG=![]() ,
,
∵直径为![]() ,
,
则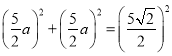 ,解得a=1,
,解得a=1,
∴AF=CM=5,
∵FH ![]() ,
,
∴FH=7,
∵OG⊥CM,AH∥CM,
∴OP⊥FH,
∴PH=![]() ,
,
在Rt△OPH中,
OP=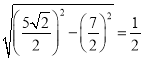 ,
,
∴MN=GP=2,
∵MN⊥AH,BC⊥AH,
∴四边形MNDC为矩形,
∴DN=CM=5,
∴FD=NH=1,
∴FN=6,
在Rt△MNF中,
FM=![]() ,
,
∵∠FBD=∠CMF,∠CMF=∠MFH,
∴∠FBD=∠MFN,
又∵∠BDF=∠FNM=90°,
∴△FBD∽△FNM,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
 ,
,