题目内容
【题目】小岛![]() 在港口
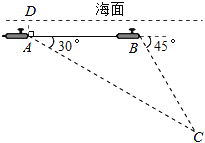
在港口![]() 的南偏西45°方向,距离港口81海里处.甲船从
的南偏西45°方向,距离港口81海里处.甲船从![]() 出发,沿
出发,沿![]() 方向以6海里/时的速度驶向港口,乙船从港口
方向以6海里/时的速度驶向港口,乙船从港口![]() 出发,沿南偏东60°方向,以15海里/时的速度驶离港口.现两船同时出发.
出发,沿南偏东60°方向,以15海里/时的速度驶离港口.现两船同时出发.
(1)出发后 小时两船与港口![]() 的距离相等;
的距离相等;
(2)出发几小时后乙船在甲船的正东方向?(结果精确到0.1小时,参考数据:![]()
【答案】(1)![]() ;(2)出发4.9小时后乙船在甲船的正东方向
;(2)出发4.9小时后乙船在甲船的正东方向
【解析】
(1)设出发后x小时两船与港口P的距离相等,转化为方程的问题解决.
(2)过点P作PE⊥CD,垂足为E.则点E在点P的正南方向,则得到相等关系,C、D两点到在南北方向上经过的距离相等,因而根据方程就可以解决.
(1)设出发后x小时两船与港口P的距离相等,
根据题意得:![]() ,
,
解这个方程得:![]() ,
,
答:出发后![]() 小时两船与港口P的距离相等;
小时两船与港口P的距离相等;
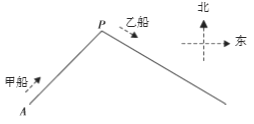
(2)设出发后y小时乙船在甲船的正东方向,
此时甲、乙两船的位置分别在点C,D处,
连接CD,过点P作PE⊥CD,垂足为E,则点E在点P的正南方向,
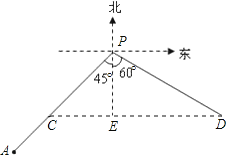
在Rt△CEP中,∠CPE=45°,
∴PE=PC![]() cos45°,
cos45°,
在Rt△PED中,∠EPD=60°,
∴PE=PD![]() cos60°,
cos60°,
∴PC![]() cos45°=PD
cos45°=PD![]() cos60°.
cos60°.
∴(81-6y)cos45°=15y![]() cos60°,
cos60°,
解得:y≈4.9.
答:出发后约4.9小时乙船在甲船的正东方向.

 阅读快车系列答案
阅读快车系列答案【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以13元/千克的价格销售,那么每天可获取利润750元.
【利润=(销售价-进价)![]() 销售量】
销售量】
(1)请根据他们的对话填写下表:
销售单价x(元/kg) | 10 | 11 | 13 |
销售量y(kg) |
(2)请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;
(3)设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?