题目内容
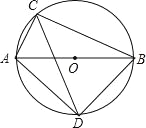
【题目】如图所示,⊙O的直径AB=10cm,弦AC=6cm,∠ACB的平分线交⊙O于点D,
(1)求证:△ABD是等腰三角形;
(2)求CD的长.
【答案】(1)详见解析;(2)CD=7![]() .
.
【解析】
(1)连接OD,根据角平分线的定义得到∠ACD=∠BCD,根据圆周角定理,等腰三角形的定义证明即可;
(2)作AE⊥CD于E,根据等腰直角三角形的性质求出AD,根据勾股定理求出AE、CE,DE,结合图形计算,即可得到答案.
(1)连接OD.
∵AB为⊙O的直径,∴∠ACB=90°.
∵CD是∠ACB的平分线,∴∠ACD=∠BCD=45°,由圆周角定理得:∠AOD=2∠ACD=90°,∠BOD=2∠BCD=90°,∴∠AOD=∠BOD=90°,∴DA=DB,即△ABD是等腰三角形;
(2)作AE⊥CD于E.
∵AB为⊙O的直径,∴∠ADB=90°,∴AD![]() AB=5
AB=5![]() .
.
∵AE⊥CD,∠ACE=45°,∴AE=CE=![]() AC=3
AC=3![]() .在Rt△AED中,DE
.在Rt△AED中,DE![]() ,∴CD=CE+DE=3
,∴CD=CE+DE=3![]() .
.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目