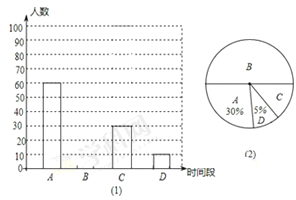
题目内容
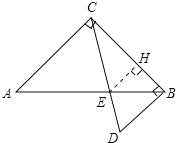
【题目】如图,将两块直角三角形的一条直角边重合叠放,已知AC=BC=![]() +1,∠D=60°,则两条斜边的交点E到直角边BC的距离是 .
+1,∠D=60°,则两条斜边的交点E到直角边BC的距离是 .

【答案】1
【解析】
试题分析:过点E作EH⊥BC,垂足为H,根据AC=BC=![]() +1,∠D=60°,得∠BCD=30°,求得BD,可证明△BDE∽△ACE,得
+1,∠D=60°,得∠BCD=30°,求得BD,可证明△BDE∽△ACE,得![]() =
=![]() ,从而得出BE和AE,再由∠ACB=90°,得△BHE∽△BCA,
,从而得出BE和AE,再由∠ACB=90°,得△BHE∽△BCA,![]() =
=![]() ,从而得出EH即可.
,从而得出EH即可.
解:∵∠CBD=90°,∠D=60°,
∴∠BCD=30°,
∴∠ACE=60°,
∵AC=BC=![]() +1,
+1,
∴BD=![]() ,AB=
,AB=![]() (
(![]() +1),
+1),
∵∠AEC=∠BED,
∴△BDE∽△ACE,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴BE=![]() ,AE=
,AE=![]() ,
,
∵∠ACB=90°,
∴△BHE∽△BCA,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴EH=1,
故答案为1.

练习册系列答案
 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目