题目内容
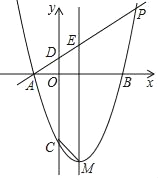
【题目】已知抛物线y=ax2+bx+c经过A(0,2),B(2,﹣2)两点.
⑴用含a的式子表示b.
⑵当a=﹣![]() 时,y=ax2+bx+c的函数值为正整数,求满足条件的x值.
时,y=ax2+bx+c的函数值为正整数,求满足条件的x值.
⑶若a>0,线段AB下方的抛物线上有一点E,求证:不管a取何值,当△EAB的面积最大时,E点的横坐标为定值.
【答案】(1)b=﹣2a﹣2;(2)x=﹣2或x=0或x=-1+![]() 或x=-1-
或x=-1-![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1)利用待定系数法建立方程组求解即可得出结论;
(2)先求出抛物线解析式,配方得:y=![]() ,由y是正整数,得出(x+1)2=1或(x+1)2=3,解方程即可得出结论;
,由y是正整数,得出(x+1)2=1或(x+1)2=3,解方程即可得出结论;
(3)根据三角形的面积的计算方法建立函数关系式,即可得出结论.
(1)∵抛物线y=ax2+bx+c经过A(0,2),B(2,﹣2),∴![]() ,∴
,∴![]() ,即:b=﹣2a﹣2;
,即:b=﹣2a﹣2;
(2)由(1)知,c=2,b=﹣2a﹣2.
∵a![]() ,∴b=﹣1,∴抛物线解析式为y
,∴b=﹣1,∴抛物线解析式为y![]() x2﹣x+2
x2﹣x+2![]() (x+1)2
(x+1)2![]() =
=![]() .
.
∵y=ax2+bx+c的函数值为正整数,即![]() 为正整数,∴(x+1)2=1或(x+1)2=3,解得:x=﹣2或x=0或x=-1+
为正整数,∴(x+1)2=1或(x+1)2=3,解得:x=﹣2或x=0或x=-1+![]() 或x=-1-
或x=-1-![]() ;
;
(3)由(1)知,c=2,b=﹣2a﹣2,∴抛物线的解析式为y=ax2﹣(2a+2)x+2.
∵A(0,2),B(2,﹣2),∴直线AB的解析式为y=﹣2x+2.
∵点E在线段AB下方的抛物线上,设点E(m,am2﹣(2a+2)m+2),过点E作y轴的平行线,交AB于F,∴F(m,﹣2m﹣2),∴EF=﹣2m﹣2﹣[am2﹣(2a+2)m+2]=﹣a(m﹣1)2+a,∴S△EAB![]() EF×|xB﹣xA|=EF=﹣a(m﹣1)2+a.
EF×|xB﹣xA|=EF=﹣a(m﹣1)2+a.
∵a>0,∴﹣a<0,∴m=1时,△EAB面积最大,即:不管a取大于0的何值,当△EAB的面积最大时,E点的横坐标为定值,定值为1.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案