题目内容
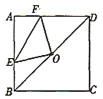
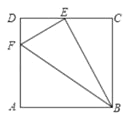
【题目】如图，在边长12的正方形ABCD中，点E是CD的中点，点F在边AD上，且AF=3DF，连接BE，BF，EF，请判断△BEF的形状，并说明理由。
【答案】△BEF是直角三角形，理由见解析
【解析】
因为正方形的四条边相等，边长为12，由E为DC的中点，得出DE和EC的长，AF=3DF，得出AF和DF的长，从而在Rt△ABF中、Rt△BCE中和Rt△DEF中，分别由勾股定理求得BF、BE和EF的长，得到BE2+EF2=BF2，再由勾股定理逆定理证得△BEF是直角三角形.
解：△BEF是直角三角形，理由如下：
∵四边形ABCD是正方形，
∴∠A=∠C=∠D=90°
∵点E是CD的中点，
∴DE=CE=
CD=6．
∵AF=3DF，
∴DF=
AD=3
∴AF=3DF=9．
在Rt△ABF中，由勾股定理可得BF2=AB2+AF2=144+81=225，
在Rt△BCE中，由勾股定理可得BE2=CB2+CE2=144+36=180，
在Rt△DEF中，由勾股定理可得EF2=DF2+DE2=9+36=45，
∵BE2+EF2=180+45=225，BF2=225，
∴BE2+EF2=BF2
∴△BEF是直角三角形.
练习册系列答案
相关题目
