题目内容
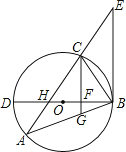
【题目】一条排水管的截面如图所示.已知排水管的半径OB=10,水面宽AB=16.求截面圆心O到水面的距离. 
【答案】解:过O作OC⊥AB垂足为C,
∵OC⊥AB
∴BC=8cm
在RT△OBC中,由勾股定理得,
OC= ![]() =
= ![]() =6,
=6,
答:圆心O到水面的距离6.
【解析】先根据垂径定理得出AB=2BC,再根据勾股定理求出BC的长,进而可得出答案.
【考点精析】利用垂径定理的推论对题目进行判断即可得到答案,需要熟知推论1:A、平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧B、弦的垂直平分线经过圆心,并且平分弦所对的两条弧C、平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧;推论2 :圆的两条平行弦所夹的弧相等.

练习册系列答案
相关题目
【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究.探究过程如下,请补充完整. 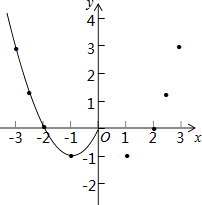
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | n |
| 3 | … |
其中,m= , n= .
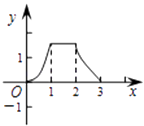
(2)根据表格数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该图象的另一部分.
(3)观察函数图象,写出两条函数的性质:①;② .
(4)进一步探究函数图象发现: ①函数图象与x轴有个交点,所以对应的方程x2﹣2|x|=0有个实数根;
②方程x2﹣2|x|=2有个实数根.