题目内容
【题目】有甲乙两名采购员去同一家饲料公司分别购买两次饲料,两次购买饲料价格分别为m元/千克和n元/千克,且m≠n,两名采购员的采购方式也不同,其中甲每次购买1000千克,乙每次用去800元,而不管购买多少饲料.
(1)甲、乙所购饲料的平均单价各是多少?(用字母m、n表示)
(2)谁的购货方式更合算?
【答案】(1)![]() ,
,![]() (2)乙的购货方式更合算
(2)乙的购货方式更合算
【解析】
⑴两次购买价格不同,m≠n,根据购买饲料的平均单价等于总价格除以购买的饲料总价,列出甲、乙所购饲料的平均单价的代数式,化简即可.
⑵由⑴化简后的代数式,可得甲乙平均单价之差的表达式,化简并将分子转化为完全平方式,根据完全平方式的非负性,判断代数式的正负,可得甲的平均单价高,所以乙更合适.
(1)解:甲两次购买饲料的平均单价为![]() ,
,
乙两次购买饲料的平均单价为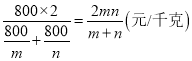
(2)解:甲、乙两次购买饲料的平均单价的差是:
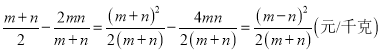
∵m、n是正数,且m≠n
∴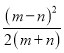 >0,
>0,
即![]() >
>![]() ,
,
∴乙的购货方式更合算.

练习册系列答案
相关题目










